Световой сигнал

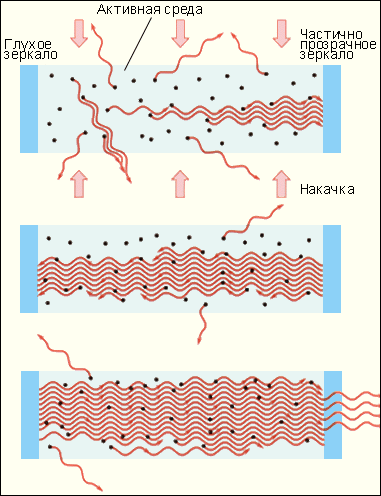
Она может служить резонансным усилителем светового сигнала. Для того, чтобы возникала генерация света, необходимо использовать обратную связь. Для этого активную среду нужно расположить между двумя высококачественными зеркалами, отражающими свет строго назад, чтобы он многократно прошел через активную среду, вызывая лавинообразный процесс индуцированной эмиссии когерентных фотонов. При этом в среде должна поддерживаться инверсная населенность уровней. Этот процесс в лазерной физике принято называть накачкой. Начало лавинообразному процессу в такой системе при определенных условиях может положить случайный спонтанный акт, при котором возникает излучение, направленное вдоль оси системы. Через некоторое время в такой системе возникает стационарный режим генерации. Это и есть лазер. Лазерное излучение выводится наружу через одно (или оба) из зеркал, обладающее частичной прозрачностью. На рис. 2 схематически представлено развитие лавинообразного процесса в лазере.

2

Рисунок 2. Развитие лавинообразного процесса генерации в лазере.

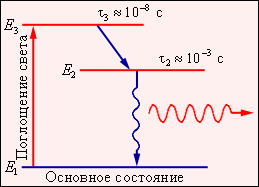
Существуют различные способы получения среды с инверсной населенностью уровней. В рубиновом лазере используется оптическая накачка. Атомы возбуждаются за счет поглощения света. Но для этого недостаточно только двух уровней. Каким бы мощным не был свет лампы–накачки, число возбужденных атомов не будет больше числа невозбужденных. В рубиновом лазере накачка производится через третий выше расположенный уровень (рис. 3).

3

Рисунок 9.4.3. Трехуровневая схема оптической накачки. Указаны «времена жизни» уровней E2 и E3. Уровень E2 – метастабильный. Переход между уровнями E3 и E2 безызлучательный. Лазерный переход осуществляется между уровнями E2 и E1. В кристалле рубина уровни E1, E2 и E3 принадлежат примесным атомам хрома.

После вспышки мощной лампы, расположенной рядом с рубиновым стержнем, многие атомы хрома, входящего в виде примеси в кристалл рубина (около 0,05 %), переходят в состояние с энергией E₃, а через промежуток τ ≈ 10^–8 с они переходят в состояние с энергией E₂. Перенаселенность возбужденного уровня E₂ по сравнению с невозбужденным уровнем E₁ возникает из-за относительно большого времени жизни уровня E₂. Лазер на рубине работает в импульсном режиме на длине волны 694 мм (темно-вишневый свет), мощность излучения может достигать в импульсе 10⁶–10⁹ Вт. Исторически это был первый действующий лазер (американский физик Т. Майман, 1960 г.). Одним из самых распространенных лазеров в настоящее время является газовый лазер на смеси гелия и неона. Общее давление в смеси составляет порядка 10² Па при соотношении компонент He и Ne примерно 10 : 1. Активным газом, на котором возникает генерация на длине волны 632,8 нм (ярко-красный свет) в непрерывном режиме, является неон. Гелий является буферным газом, он участвует в механизме создания инверсной населенности одного из верхних уровней неона. Излучение He–Ne лазера обладает исключительной, непревзойденной монохроматичностью. Расчеты показывают, что спектральная ширина линии генерации He–Ne лазера составляет примерно Δν ≈ 5·10^–4 Гц. Это фантастически малая величина.

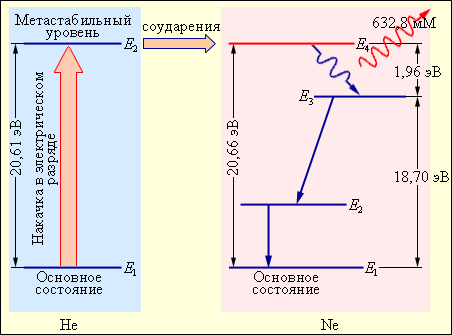
Время когерентности такого излучения оказывается порядка τ ≈ 1 / Δν ≈ 2·10³ с, а длина когерентности cτ ≈ 6·10¹¹ м, то есть больше диаметра земной орбиты! На практике многие технические причины мешают реализовать столь узкую спектральную линию He–Ne лазера. Путем тщательной стабилизации всех параметров лазерной установки удается достичь относительной ширины Δν / ν порядка 10^–14–10^–15, что примерно на 3–4 порядка хуже теоретического предела. Но и реально достигнутая монохроматичность излучения He–Ne лазера делает этот прибор совершенно незаменимым при решении многих научных и технических задач. Первый гелий-неоновый лазер был создан в 1961 году. На рис.4 представлена упрощенная схема уровней гелия и неона и механизм создания инверсной населенности лазерного перехода.

4

Рисунок 4. Механизм накачки He–Ne лазера. Прямыми стрелками изображены спонтанные переходы в атомах неона.

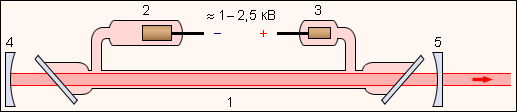
Накачка лазерного перехода E₄ → E₃ в неоне осуществляется следующим образом. В высоковольтном электрическом разряде вследствие соударений с электронами значительная часть атомов гелия переходит в верхнее метастабильное состояния E₂. Возбужденные атомы гелия неупруго сталкиваются с атомами неона, находящимися в основном состояние, и передают им свою энергию. Уровень E₄ неона расположен на 0,05 эВ выше метастабильного уровня E₂ гелия. Недостаток энергии компенсируется за счет кинетической энергии соударяющихся атомов. На уровне E₄ неона возникает инверсная населенность по отношению к уровню E₃, который сильно обедняется за счет спонтанных переходов на ниже расположенные уровни. При достаточно высоком уровне накачки в смеси гелия и неона начинается лавинообразный процесс размножения идентичных когерентных фотонов. Если кювета со смесью газов помещена между высокоотражающими зеркалами, то возникает лазерная генерация. На рис. 5 изображена схема гелий-неонового лазера.

5

Рисунок 5. Схема гелий-неонового лазера: 1 – стеклянная кювета со смесью гелия и неона, в которой создается высоковольтный разряд; 2 – катод; 3 – анод; 4 – глухое сферическое зеркало с пропусканием менее 0,1 %; 5 – сферическое зеркало с пропусканием 1–2 %.

Современные высокостабильные гелий-неоновые лазеры производятся в моноблочном исполнении. Для этого используется стеклообразное вещество – ситалл, обладающий практически нулевым температурным коэффициентом расширения. В куске ситалла в форме прямоугольного параллелепипеда просверливается канал, к торцам которого на оптическим контакте приклеиваются лазерные зеркала. Канал заполняется смесью гелия и неона. Катод и анод вводятся через дополнительные боковые каналы. Такая моноблочная конструкция обеспечивает высокую механическую и тепловую стабильность.

Слово «когерентность» — греческого происхождения и в наиболее общем смысле означает «согласованность». Простейший пример: когда по улице прогуливается толпа людей, она идёт некогерентно, а когда марширует рота солдат, то она идёт когерентно.

Когерентные волны — это волны оди­наковой частоты, между которыми сохра­няется постоянная разность фаз, (то есть они согласованы по фазе). При сложении двух когерентных волн одинаковой поля­ризации (с одним и тем же направлением колебаний напряженности электрического поля) амплитуда суммарной волны зави­сит от разности фаз складываемых волн — это и есть интерференция.

При интерференции световых волн удобнее иметь дело не с амплитудами, а с интенсивностями. Это не меняет су­щества дела, так как интенсивность про­порциональна квадрату амплитуды. Если в какую-либо точку приходят две волны с интенсивностями I₁и I₂ и фазами φ₁ и φ₂ соответственно, то результирующая интенсивность в этой точке определяется выражением

I_рез =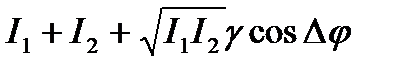

где Δφ = | φ₁— φ₂ | — разность фаз, а мно­житель γ отражает с тепень когерентности волн. Из этой формулы наглядно видна за­висимость результирующей интенсивно­сти от разности фаз Δφ и от величины γ.

В тех местах, куда волны приходят в одинаковой фазе, то есть «гребни» и «впадины» одной волны совпадают с «гребнями» и «впадинами» другой (Δφ=0, cos Δφ = 1), волны усиливают одна дру­гую и наблюдается максимальная интен­сивность (I_тах). В тех местах, куда волны приходят в противофазе, «гребни» одной волны совпадают со «впадинами» другой (Δφ = 180°, cos Δφ = —1), волны гасят одна другую и результирующая интенсивность становится минимальной (I_min ). Таким образом, образуется интерференционная картина, состоящая из чередующихся светлых и тёмных участков.

Когерентность волн определяет их спо­собность к интерференции.

Теперь, прояснив наиболее существен­ные моменты, касающиеся интерферен­ции, перейдём к нашей основной теме.

Существует множество интерференци­онных схем (интерферометров), но до­статочно рассмотреть только одну из них. Вернёмся к уже знакомой схеме интерфе­рометра Юнга (рис. 1). На экране наблюда­ется интерференционная картина. Будем постепенно уменьшать интенсивность света. Освещённость экрана станет падать, но интерференционная картина сохранит­ся. Продолжим уменьшать интенсивность света, а вместо экрана поставим фотопла­стинку, потому что глазом уже ничего не видно (рис. 2). Увеличив время экспозиции и проявив пластинку, обнаружим на ней всё ту же интерференционную картину (на рис. 2 это показано кривой D, отображаю­щей интерференционное распределение полос). Уже интересно: значит, интерфе­ренция не зависит от интенсивности света? Продолжаем опыт, все больше уменьшая интенсивность и соответственно увеличи­вая время экспозиции.

Короче говоря, при достаточно длительной экспозиции можно обнаружить интерференционную кри­вую D в принципе при сколь угодно малой интенсивности света. Но с уменьшением ин­тенсивности светового пучка уменьшается число фотонов в нем, и наступит такой мо­мент, когда вместо световых волн в интерферометр Юнга будут поступать отдельные фотоны. Вот излучился один фотон, за ним другой и т.д. — фотоны поступают в интерферометр сугубо поодиночке. Но при этом сохраня­ется интерференционный характер кривой D,на фотопластинке получается такая же интерференционная картина, как и от световых волн!

Как же это может быть? Ведь для полу­чения интерференции необходимо, чтобы свет поступал на пластинку одновременно от двух отверстий 1 и 2. Но отдельный фотон не может пройти сразу через оба отверстия. Он проходит либо через отверстие 1, либо через отверстие 2. Очевидно также, что он не может разделиться на две «половинки». И вот тут мы сталкиваемся с совершенно мистической ситуацией. Фотон проходит через одно отверстие, но эффект такой, как будто он прошёл через два. Это приводит к парадоксальному утверждению: нельзя считать, что фотон проходит через одно отверстие независимо отдругого. Если бы это было так, то при прохождении, скажем, через отверстие 1 было бы совершенно безразлично, откры­то или закрыто отверстие 2. Но если мы закроем отверстие 2, то, как показывает опыт, интерференционная картина не­медленно исчезнет!

Всё это очень странно. Более того — не­постижимо. Но вернёмся к схеме Юнга — нас ждёт ещё много интересного.

Итак, мы имеем дело с отдельными фотонами. Закроем отверстие 2. Теперь мы точно знаем, что фотоны проходят только через отверстие 1. Интерференция исчезает, и распределение попаданий фотонов на фотопластинку за некоторый достаточно большой интервал времени описывается кривой А (рис. 2). Теперь откроем отверстие 2 и закроем 1. Фотоны будут проходить только через открытое от­верстие 2, и их распределение отобразится кривой В. Теперь откроем оба отверстия. Если, как этого требует логика, считать, что каждый фотон проходит либо через одно, либо через другое отверстие, то на фотопластинке-детекторе должна зафик­сироваться сумма этих распределений, то есть кривая С (обозначенная на рис. 2 пунктиром). Но возникает не суммарное, а интерференционное распределение D. То есть фотон при прохождении того или другого отверстия каким-то образом «ощущает» соседнее отверстие; в противном случае, как уже говорилось, фотону было бы «безразлично», открыто или закрыто соседнее отверстие, и при обоих открытых отверстиях должна была бы фиксироваться суммарная кривая С. Это удивительное появление интерференции при прохождении фотонов через одно отверстие - чисто квантовый эффект, один из парадоксов квантовой механики, который невозможно объяснить на основе классической теории.

Но пойдем дальше. Описанный эффект наблюдается не только с фотонами, но и с электронами, протонами, нейтронами, то есть с микрообъектами (подобные эксперименты производились неоднократно). Особенно наглядными были опыты с электронами, которые вроде бы уж точно «частицы», а не волны. И вот физики придумали, как «подглядеть», каким образом электрон проходитчерез отверстия. Они поместили вблизи каждого отверстия по источнику света и фотоприёмнику, расположив их так, что приёмники регистрируют свет, рассеянный электроном. Если электрон проходит через одно отверстие, сработает один фотоприёмник, и мы узнаем, через какое отверстие прошёл электрон; если же он непостижимым образом пройдет сразу через оба отверстия, то сработают оба фотоприемника. Что же дал такой опыт? Оказалось, что всегда срабатывает только один фотоприёмник и никогда не оба одновременно. Значит электрон всегда проходит только через одно отверстие, и мы всегда можем сказать через какое именно. Что же получается? Что электрон, проходя через одно отверстия каким-то образом «ощущает» другое?

Но давайте наберём достаточно число попаданий электронов на разные места экрана и посмотрим, как распределятся эти попадания. (В случае электронов вместо фотопластинки используется передвижной детектор, например счетчик Гейгера или другое устройство, откликающееся при попадании на него, скажем, щелчком в динамике.) И тут обнаруживается совершенно неожиданная вещь. Кривая распределения оказывается не интерференционной, а суммарной. А если мы уберём источники света и фотоприёмники, то получится интерференционная кривая. Другими словами «подглядеть» за электронами разрушает их интерференцию!

Но может быть, освещая электроны, мы изменили их движение? Вполне возможно: ведь фотоны света, сталкиваясь с электронами, оказывают на них какое-то воздействие. Наверное, надо как-то уменьшить это воздействие до практически пренебрегаемого, чтобы интерференци­онная картина не разрушалась. Но как? Уменьшить интенсивность подсветки? Это ничего не даст, так как при этом будет уменьшаться число фотонов в пучке, и если мы добьёмся испускания света от­дельными фотонами, то просто возрастёт количество «незарегистрированных» электронов. Нужно уменьшать не интен­сивность, а энергию фотонов. Однако для этого есть только один путь — увеличи­вать длину волны света или, что то же, уменьшать частоту световых колебаний: энергия фотона (кванта света) Е связана с оптической частотой ν соотношением Е = hν где h — постоянная Планка. Зна­чит, чем больше длина волны, тем мень­ше её энергия и тем слабее воздействие на электрон. Самый длинноволновый свет в видимой области — красный; ещё лучше взять инфракрасное излучение, у которого длина волны может быть гораздо больше. Но — увы! — этот путь тоже оказывается тупиковым. Ибо, как только длина волны сравняется с рассто­янием между отверстиями, невозможно будет разобрать, возле какого отверстия произошла вспышка. Если длина волны будет намного превышать расстояние между отверстиями — вот тогда воз­мущение, оказываемое светом, станет настолько слабым, что снова появится интерференционная кривая, но при этом не окажется никакой возможности уста­новить, куда прошёл электрон.

Предпринималось ещё много попыток придумать опыт, который позволил бы «наблюдать» за электронами без разруше­ния интерференции, но ни одна из них не увенчалась успехом.

Мы рассмотрели эту проблему с чисто ка­чественной стороны, ибо строгое аналити­ческое рассмотрение требует знакомства с математическим аппаратом квантовой ме­ханики. Поэтому ограничимся сказанным, из которого следует вывод: при интерфе­ренции отдельных фотонов, электронов и прочих микробъектов любые попытки про­следить, как она образуется, немедленно разрушают интерференционную картину. Почему природа не позволяет нам понять механизм подобного явления — на этот во­прос не может ответить никто, по крайней мере в настоящее время. И здесь уместно привести слова выдающегося американ­ского физика Ричарда Фейнмана: «Мы говорим «в настоящее время», но мы очень серьёзно подозреваем, что всё это — уже навсегда и разгрызть этот орешек человеку не по зубам, ибо такова природа вещей».

[1] Надо дать волне время, чтобы дойти от точки О до точки А.

* Камертон это такая штука, похожая на вилку с двумя зубцами, только зубцы широкие, так что есть им неудобно. Сделан он из какого-либо твердого цветного сплава. Если по зубцам стукнуть они начнут колебаться и камертон зазвучит. В общем вроде колокола, только маленький.

[2] Ну не всегда это одно и то же.

[3] Несомненно вы заметили, что предыдущие рассуждения очень похожи на те, которые мы приводили, когда говорили о волнах в упругих средах.

1 Ну совсем как в политике.

1 1 нм (нанометр) равен 10^-9 м.

1 Группой волн называют импульс, который можно представить в виде совокупности бесконечного числа синусоид, частоты которых мало отличаются друг от друга.

1 Знак минус означает, что углы i’ и i отсчитываются в разные стороны от нормали к поверхности.