Механика теории относительности.
Рассуждения, приведенные выше, показывают, что оптические (и электромагнитные) явления подтверждают кинематику теории относительности, вытекающую из преобразований Лоренца. Естественно ожидать, что эти кинематические законы, дающие пространственно-временную характеристику явлений, должны быть одинаковыми для всех явлений природы. Поскольку преобразования Галилея, относительно которых инвариантны законы ньютоновской механики, являются предельными выражениями преобразований Лоренца, при стремлении отношения υ/'с к нулю, можно думать, что уравнения механики Ньютона также являются предельными уравнениями некоторых более общих уравнений, инвариантных по отношению к преобразованиям Лоренца, как того требует теория относительности.
Найти вид уравнений механики теории относительности можно, внеся в уравнения Ньютона такие изменения, которые делают их инвариантными по отношению к преобразованиям Лоренца.
Напишем уравнение механики Ньютона в векторной форме:
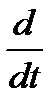 (mv) = f(1)
(mv) = f(1)
В механике Ньютона масса т считается величиной постоянной, независящей от состояния движения. Как можно показать, это предположение не совместимо с требованием инвариантности уравнений по отношению к преобразованию Лоренца. Требование, чтобы в механике теории относительности, как и в механике Ньютона, для изолированной системы тел выполнялся в любой системе закон сохранения количества движения и учет законов преобразования скоростей при переходе из одной системы в другую, приводит к выводу, что масса тела должна иметь разные значения в разных системах, находящихся в относительном движении. Закон преобразования масс при этом окажется следующим:
m = m0 / 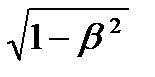 (2)
(2)
Здесь т0 есть значение массы, измеренной в системе, в которой она покоится, а т — значение той же массы, измеренной в системе, движущейся относительно первой с постоянной скоростью υ. Уравнения механики окажутся инвариантными по отношению к преобразованиям Лоренца, если в формуле (1) под массой т подразумевать величину, преобразующуюся по закону (2). Таким образом, уравнения механики теории относительности принимают форму:
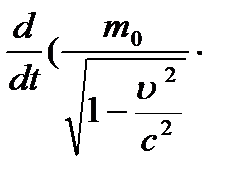 v) = f(3)
v) = f(3)
Очевидно, что эти уравнения, отличающиеся от уравнений Ньютона, должны приводить к иным следствиям, чем уравнения классической механики. Проверка этих следствий на опыте является проверкой и самих уравнений.
Как известно, в классической механике уравнение движения может быть записано в виде: 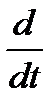 p = f, где , р — количество движения. Сравнивая его с (3), видим, что в механике теории относительности роль количества движения играет величина:
p = f, где , р — количество движения. Сравнивая его с (3), видим, что в механике теории относительности роль количества движения играет величина:
p=m0v/ 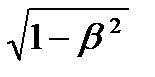 =mv(4)
=mv(4)
Исключительно важным следствием механики теории относительности является вытекающая из нее связь между энергией и массой. Установим это соотношение, основываясь на формуле (3). В классической механике изменение кинетической энергии материальной точки определяется по работе, совершенной силами, приложенными к точке. Проведем соответственное рассмотрение для уравнения (3). Элементарная работа dА силы f равна скалярному произведению силы на перемещение dr точки:
dA=f· dr.
Эта величина должна давать приращение кинетической энергии точки:
dA =dEk .
На основании формулы (3) имеем:
dEk = dA = 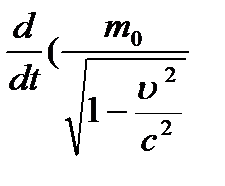 v) · dr
v) · dr
Выполняя дифференцирование, получим:
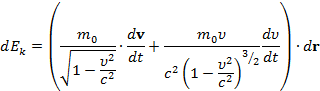
или, так как dr/dt равно скорости v, то
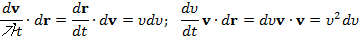
Следовательно:
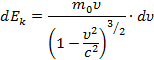
С другой стороны, по формуле (2) находим:
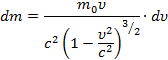
Из сопоставления двух последних формул получаем следующую связь между dEk и dт:
dEk = c2dm (5)
Изменение энергии пропорционально изменению массы, причем коэффициентом пропорциональности является квадрат скорости света. Это положение естественно обобщить, считая что между энергией Е и массой т имеется общая связь, выражаемая соотношением:
Е = тс2(5а)
Масса и энергия являются характеристиками качественно различных свойств тех видов материи, которые рассматривает физика. Масса характеризует инерционные свойства материи (второй закон Ньютона) и свойства, проявляющиеся в явлениях всемирного тяготения. Энергия является величиной, изменение которой определяет совершаемые системой работы. Вытекающие из теории относительности соотношения (5) и (5а) указывают, что между этими двумя характеристиками имеет место связь: изменение одной из них ведет к эквивалентному изменению другой. Изменение массы системы может произойти не только за счет обмена с внешними телами веществом (атомами, молекулами), но и за счет передачи системе энергии. Например, если системе передается количество тепла ΔQ, в результате чего ее энергия возрастает на величину ΔЕ, то в соответствии с соотношением (5) одновременно возрастает и масса системы на величину Δm=ΔE/c2.
Другой пример: если в результате излучения света энергия системы убывает на ΔЕ, то одновременно уменьшается ее масса на величину Δm=ΔE/c2. Для замкнутой системы сохраняется ее масса и сохраняется ее полная энергия.
Ввиду большого численного значения скорости света с в пустоте, определенному численному изменению энергии ΔЕ соответствует малое изменение массы Δm. При увеличении энергии системы Е на 1 дж ее масса увеличивается лишь на Δm ≈ 1,1 • 10-14 г. Поэтому при обычных изменениях энергии тел изменение их массы настолько мало, что оно не может быть непосредственно замечено. Однако современная физика имеет возможность проверить соотношение между энергией и массой, благодаря огромным количествам энергии, освобождаемым при ядерных превращениях.
Из соотношения между энергией и массой вытекает релятивистская форма связи между энергией и количеством движения. Подставив в (5а) вместо т его значение по (2), получим:
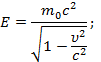
возводя это равенство в квадрат и производя алгебраические преобразования, найдем:
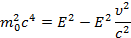
или на основании (4):
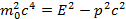
Дата добавления: 2015-06-12; просмотров: 840;
