Тангенс угла диэлектрических потерь.Для оценки соотношения между током проводимости и током смещения удобно ввести величину тангенс угла диэлектрических потерь
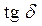 =
= 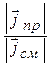 =
=  . (2.15)
. (2.15)
В зависимости от значения tgd среды можно классифицировать так:

 (2.16)
(2.16)
Из уравнения (2.15) следует, что tgd зависит от частоты. Это значит, что одно и то же вещество может на НЧ вести себя как проводник, а на ВЧ – как диэлектрик.
Например, морская вода с параметрами s = 1 См/м и e = 80 на частотах менее 23 МГц проявляет себя как проводник, а на частотах более 2,3 ГГц – как диэлектрик. Следует отметить, что такие типичные диэлектрики, как фарфор, эбонит, слюда, из-за очень малой проводимости (s <10–12 См/м) даже на очень низких частотах остаются диэлектриками, а металлы из-за очень высокой проводимости(s >106 См/м) остаются проводниками на высоких частотах вплоть до диапазона КВЧ.
При измерениях на высоких частотах tgd обычно оказывается больше, чем результаты по уравнению (2.15). Это происходит в основном из-за влияния поляризационных потерь [1, 11], которые суммируются с tgd (2.15). Для типичных радиодиэлектриков на высоких частотах именно данный вид потерь является преобладающим [2], поэтому более точным будет определение tgd как отношения активной части плотности полного тока смещения к реактивной [1, 2]
 , (2.17)
, (2.17)
где yЭ – угол запаздывания по фазе  от
от 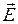 [1, 2].
[1, 2].
Система уравнений Максвелла с учетом сторонних источников.В задачах электродинамики к сторонним источникам относят такие источники ЭМП, которые возбуждают это поле, но сами от него не зависят, так как их поддерживают сторонние по отношению к исследуемому ЭМП физические явления [11]. Например, при определении ЭМП вокруг проволочной антенны целесообразно исключить из анализа ЭМП генератор и линию передачи, которые вместе с антенной образуют единую электродинамическую систему, а влияние происходящих в них процессов учесть введением в систему плотности стороннего тока, что существенно упрощает решение задачи [11].
Таким образом, сторонние величины (jст, rст и т. п.) суммируются (или вычитаются, в зависимости от направления взаимодействия токов или полярностей зарядов) с соответствующими величинами системы уравнений Максвелла.
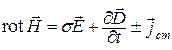 ;
; 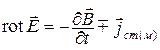 ; (2.18)
; (2.18)
 ;
; 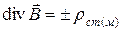 . (2.19)
. (2.19)
В комплексной форме уравнения (2.18)–(2.19) будут иметь вид
 ;
; 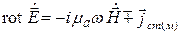 ; (2.20)
; (2.20)
 ;
;  . (2.21)
. (2.21)
Индексы (м) указывают источники магнитного типа. Введение эквивалентных (физически фиктивных) магнитных зарядов и токов может упростить решение некоторых электродинамических задач.
Список рекомендуемой литературы:[1, гл. 3, с. 17–23; 2, с. 28–39; 3, гл. 1–2, с. 16–21; 4, с. 16–21; 5, с. 8–13, 17–18; 6, с. 7–41, 119–121; 7, с. 34–49; 8, с. 5–7; 9, с. 30–38, 51–56; 10, с. 19–38, 51–56; 11, с. 16–42, 48–52; 12, с. 26–37, 46–54; 13, с. 8–29, 36–39, 123–128; 15, с. 199–207; 31].
Контрольные вопросы и задания
1. Запишите систему уравнений Максвелла в интегральной форме, укажите физическое содержание каждого уравнения системы.
2. Запишите систему уравнений Максвелла в дифференциальной форме, укажите физическое содержание каждого уравнения системы.
3. Какая форма уравнений Максвелла (дифференциальная или интегральная) лучше отражает свойства ЭМП?
4. Представляет ли система уравнения Максвелла лишь результат обобщения экспериментальных данных?
5. Какое уравнение Максвелла описывает закон ЭМ индукции?
6. Какое уравнение Максвелла обобщает закон Био – Савара?
7. Почему теорема Гаусса не используется для определения электрической индукции, когда ЭМП зависит от времени?
8. В чем смысл уравнения непрерывности?
9. На какие классы можно разделить среды по tgd ?
10. Дайте определение «стороннего» источника.
11. Как влияние сторонних источников учитывают в уравнениях Максвелла?
12. Существуют ли реально источники магнитного поля?
Дата добавления: 2015-06-12; просмотров: 1305;
