ОДНОРОДНОЙ ИЗОТРОПНОЙ СРЕДЕ

Рассмотрим безграничное трехмерное пространство, в котором распространяется электромагнитная волна. При этом будем полагать, что среда, заполняющая это пространство, является однородной, изотропной и линейной. Это значит, что свойства его не зависят от координат, направления распространения и амплитуды волны. Для такого пространства мы получили математическое описание зависимости векторов напряженности электрического и магнитного поля от координаты z и времени t. Это формула (3.6) и (3.7).

Пусть вектор напряженности электрического поля направлен по оси х. Тогда его можно описать следующим образом:

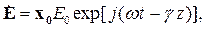
	(4.1)
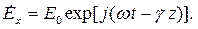
	(4.2)

Эти формулы по-разному описывают один и тот же вектор: он комплексный, направлен по оси х и имеет амплитуду Е₀. Они полностью эквивалентны. В дальнейшем мы чаще всего будем пользоваться второй формой (4.2).

Функция времени и расстояния в круглых скобках – текущая фаза волны. Она является текущей, то есть переменной, потому, что зависит от времени t и расстояния z. Какой бы из этих параметров не изменился, фаза также изменится, «утечет». Кроме того, фаза зависит и от свойств среды, в которой распространяется электромагнитная волна. Свойства среды учитываются волновым числом, в формулах (4.1) и (4.2) – комплексным.

Это полное описание вектора напряженности электрического поля с использованием комплексных чисел. Однако часто, особенно в средах без потерь, удобно пользоваться мгновенными значениями напряженности поля волны. Для того чтобы перейти к мгновенному значению, надо взять действительную часть формулы (4.2). Кроме того положим, что потерь в среде нет. Получим:

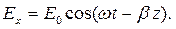
(4.3)

Переход к соотношению (4.3) выполнен с помощью формулы Эйлера, которая позволяет преобразовать экспоненциальную форму представления комплексного числа в тригонометрическую:

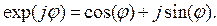
(4.4)

Действительная часть формулы (4.4) - косинус. Кроме того, в формуле (4.3) учтено, что в среде без потерь волновое число γ – действительное и равно коэффициенту фазы β.

Формула (4.3) описывает мгновенное значениеплоской монохроматической волны, распространяющейся вдоль оси z:

· значение мгновенное потому, что описывает величину напряженности электрического поля в фиксированный момент времени в фиксированной точке пространства.

· волна распространяется вдоль оси z потому, что только от этой координаты зависит ее фаза;

· волна плоская потому, что фаза постоянна на плоскости, описываемой уравнением ωt - βz = const;

· волна монохроматическая потому, что зависимость фазы от времени и координаты описывается гармонической функцией cos, которая монохроматическая по определению.

Для проведения расчетов с использованием метода комплексных амплитуд необходимо из формулы (4.2) выделить комплексную амплитуду напряженности электрического поля. Получим:

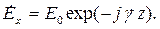
(4.5)

Для того чтобы полностью описать электромагнитную волну надо найти комплексную амплитуду напряженности магнитного поля. Это можно сделать двумя способами. Можно воспользоваться решением однородного волнового уравнения для вектора напряженности магнитного поля, полученным в главе 3. Математически это правильно, а физически не слишком. Дело в том, что полученные таким образом описания электрической и магнитной составляющих электромагнитного поля волны не будут связаны между собой. Они не будут учитывать тот факт, что переменное электрическое поле порождает переменное магнитное поле и наоборот. Значит, эти решения надо будет объединять дополнительно.

Поэтому для нахождения комплексной амплитуды вектора напряженности магнитного поля правильнее воспользоваться вторым уравнением Максвелла:

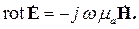
(4.6)

Из него необходимо выразить вектор напряженности магнитного поля:

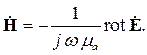
(4.7)

Теперь подставим сюда комплексную амплитуду вектора напряженности электрического поля (4.5) и раскроем оператор rot. После простейших преобразований получим:

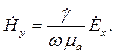
(4.8)

Таким образом, мы задали характеристики вектора напряженности электрического поля и по ним нашли вектор напряженности магнитного поля. Вектор напряженности электрического поля мы направили по оси х, а вектор напряженности магнитного поля получился направленным по оси у. Следовательно, векторы напряженности электрического и магнитного полей ортогональны.

Векторы напряженности электрического и магнитного полей взаимно перпендикулярны

Формулируя задачу, мы условились о том, что волна распространяется вдоль оси z, а векторы напряженности поля получились направленными по осям х и у, то есть перпендикулярно направлению распространения. Следовательно, мы получили поперечную волны.

Плоские электромагнитные волны в свободном пространстве являются поперечным

Формула (4.8) учитывает параметры среды, которые определяют волновое число и абсолютную магнитную проницаемость. Из нее следует, что между векторами напряженности электрического и магнитного поля существует очевидная пропорциональность:

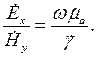
(4.9)

Определим размерность этого отношения. Это проще всего сделать по левой части формулы. Размерность напряженности электрического поля в числителе В/м, а размерность напряженности магнитного поля в знаменателе – А/м. Следовательно, размерность результата деления будет В/А, то есть Ом. Поэтому отношение комплексных амплитуд векторов напряженности электрического и магнитного полей назвали волновым сопротивлением:

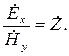
(4.10)

Волновым сопротивлением среды называется отношение комплексных амплитуд векторов напряженности электрического и магнитного полей

В общем случае векторы напряженности электрического и магнитного поля имеют проекции на обе оси координат. У вектора напряженности электрического поля может появится проекция на ось у, а у вектора напряженности магнитного поля – проекция на ось х. Если волновое сопротивление сформировать из отношения второй пары проекций, модуль его не изменится, но появится знак минус:

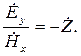
(4.11)

Таким образом, волновое сопротивление в общем случае описывается следующей формулой:

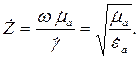
(4.12)

Из этой формулы следует весьма важный вывод.