Объяснение диамагнетизма

К диамагнетикам относятся только те вещества, у которых суммарный магнитный момент атомов (молекул) в отсутствии внешнего поля равен нулю. Рассмотрим поведение электронной орбиты в магнитном поле. Движущийся по орбите электрон подобен волчку – ему свойственно поведение гироскопа под действием внешней силы. На орбиту электрона как на замкнутый контур с током (рис. 6.2) действует вращающий момент силы (см. (3.22)): .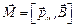

Направление вектора 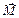можно определить как направление поступательного движения правого винта при его вращении от направления первого сомножителя в векторном произведении ( 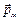) ко второму ( 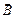). Модуль момента си­лы .

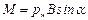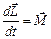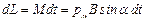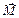По основному закону вращательного движения (см. раздел "Механика") . Под действием момента силы M за время dt момент импульса электрона изменится на величину . Поскольку вектор направлен так же, как , т.е. перпендикулярно 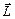, то через время dt момент импульса изменится только по направлению. Новое положение оси электронной орбиты показано на рис. 6.2 штриховой линией. Плоскость, в которой расположены ось орбиты и векторы 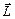и 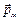, за время dt повернется на угол 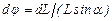. Таким образом, с течением времени концы векторов 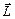и 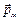будут описывать окружности (на рис. 6.2 показаны штриховыми линиями) с угловой скоростью

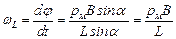. С учетом (6.1) имеем: 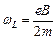. (6.2)

Рассмотренное явление называют ларморовой прецессией, а частоту (6.2) – ларморовой частотой.

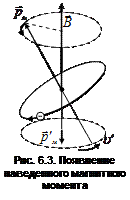
Поскольку ось электронной орбиты в результате прецессии вращается в направлении, противоположном скорости электрона, это эквивалентно движению электрона в противоположном направлении со скоростью u ' (рис. 6.3). За счет этого движения появляется наведенный магнитный момент 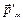, противоположный внешнему полю .

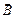Чем больше магнитная индукция поля, тем выше частота прецессии и тем больше наведенный момент. Следовательно, намагниченность (по модулю) пропорциональна магнитной индукции в полном соответствии с (5.15).

Внутри атома нет причин, по которым прецессия могла бы затухать, поэтому наведенные моменты существуют все время, пока существует поле. Тепловое движение и столкновения атомов не влияют на прецессию существенным образом. Поэтому магнитная восприимчивость диамагнетиков не зависит от температуры.

Прецессия прекращается, когда исчезает поле. Тогда же исчезают и наведенные моменты.

6.3. Объяснение парамагнетизма

Атомы (молекулы) парамагнетика в целом обладают некоторым магнитным моментом. При внесении парамагнетика в магнитное поле наблюдается прецессия электронных орбит, приводящая к появлению наведенного магнитного момента, противоположного полю (как и у диамагнетиков). Однако в парамагнетиках наблюдается другой, более сильный эффект – установление магнитных моментов атомов по внешнему полю. Прецессия магнитных моментов атомов вследствие их столкновений друг с другом быстро затухает и углы между векторами 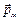и 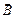уменьшаются. Тепловое движение, с одной стороны, способствует затуханию прецессии атомных моментов, с другой стороны, разбрасывает направления магнитных моментов атомов. В результате магнитные моменты атомов оказываются ориентированными преимущественно под острыми углами к направлению магнитной индукции. За счет этого внутри парамагнетика возникает собственное поле, направленное в ту же сторону, что и внешнее.

Классическая теория парамагнетизма была создана Ланжевеном в 1905 г. Поскольку ориентирующее действие поля на магнитные моменты атомов пропорционально произведению p_мВ₀, а разбрасывающее действие теплового движения характеризуется его энергией (~ kT), то результирующее действие будет определяться величиной .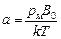

Ланжевен, решив статистическую задачу о поведении магнитных моментов атомов в магнитном поле, нашел, что намагниченность парамагнетика есть некоторая функция величины а: 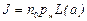, (6.3)

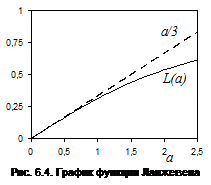
где 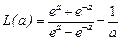- классическая функция Ланжевена, n₀ – концентрация атомов (молекул). В случае слабого магнитного поля (а<<1) L(a) = a/3 (см. рис. 6.4.). При этом условии поляризованность зависит от магнитной индукции линейно. Подстановка значения функции Ланжевена в (6.3) дает следующее выражение: 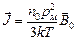. Сопоставляя данное выражение с (5.15), находим выражение для магнитной восприимчивости: 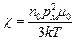. (6.4)

Видно, что магнитная восприимчивость парамагнетика обратно пропорциональна абсолютной температуре. Такая зависимость была обнаружена П.Кюри еще до разработки теории и получила название закона Кюри.

В очень сильных полях (а>1), когда функция Ланжевена становится нелинейной (рис. 6.4), наблюдаются отступления от пропорциональности между намагниченностью и магнитной индукцией. При а>>1намагниченность практически не возрастает с увеличением магнитной индукции, так как L(a) » 1 и магнитные моменты всех атомов выстраиваются по полю (такое состояние называется насыщением). Однако такие сильные магнитные поля в реальности создать невозможно, и условие а>>1является невыполнимым.

Некоторые металлы, например щелочные, не подчиняются закону Кюри. Объяснение этому было дано Паули в 1927 г. Он предположил, что парамагнетизм в этих случаях обусловлен не магнитными моментами ионов кристаллической решетки, а спиновыми магнитными моментами электронов проводимости. Эти электроны не подчиняются классической статистике Максвелла-Больцмана. Рассматривая электроны как газ, подчиняющийся статистике Ферми-Дирака, Паули рассчитал его магнитную восприимчивость.

6.4. Ферромагнетизм

Вещества, способные намагничиваться весьма сильно, получили название ферромаг­нетиков. К ферромагнетикам относятся железо, кобальт, никель, гадолиний и их сплавы. Магнитная проницаемость большинства ферромагнетиков при обычных температурах измеряется многими сотнями и тысячами единиц, а у некоторых специально приготовленных и обработанных ферромагнетиков она достигает миллиона.

Ферромагнетики, помимо способности сильно намагничиваться, обладают рядом свойств, существенно отличающих их от диа- и парамагнетиков.

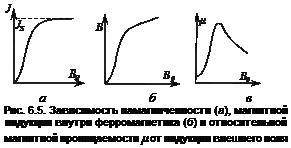Кривая намагничивания.Характерной особенностью ферромаг­нетиков является сложная нелинейная зависимость между намагниченностью J и индук­цией внешнего поля В₀ (рис. 6.5а). Намагниченность сначала быстро воз­растает, но затем наступает магнитное насыщение, при котором намагниченность достигает некоторого максимального значения J_s и практически перестает зависеть от индукции внешнего поля. В соответствии с (5.17) магнитная индукция в ферромагнетике В сначала растет быстро, а затем, в состоянии насыщения, растет только за счет роста индукции внешнего поля (рис. 6.5б).

Вследствие нелинейной зависимости В от В₀ магнитная прони­цаемость зависит от индукции внешнего магнитного поля (рис. 6.5в): вначале она возрастает с увеличением поля от начального значения до некоторой максимальной величины, но затем, после прохождения через максимум, уменьшается и асимптотически стремится к значению, близкому к единице в очень сильных полях.

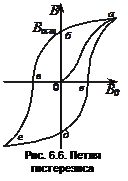
Гистерезис.Если пер­воначально не намагничен­ный ферромагнетик по­местить внутрь намаг­ничивающей катушки и уве­личивать магнитное поле, то индукция внутри магнетика будет изменяться, как было показано на рис. 6.5б, т. е. по кривой 0а на рис. 6.6.

Если теперь уменьшать магнитное поле, то уменьшение индукции будет изоб­ражаться уже другой кривой - аб. Когда внешнее поле уменьшится до нуля, ферромагнетик останется намагниченным. Индукция поля в этом состоянии называется остаточной индукцией[1]. Для того чтобы поле внутри ферромагнетика стало равным нулю, к нему необходимо приложить внешнее поле противоположного направления (точка в на рис. 6.6). Дальнейшее увеличение поля приводит кривую в точку г, затем при уменьшении до нуля - в точку д; при еще одной смене направления внешнего поля - в точки д, е и а. При циклическом перемагничивании ферромагнетика изменение индукции в нем будет изображаться петлеобразной замкнутой кривой. Такое явление называется гистерезисом, а кривая – петлей гистерезиса.

Температура Кюри. Для всякого ферромагнетика существует определенная температура T=Т_К, называемая температурой или точкой Кюри, при превышении которой ферромагнетик становится парамагнетиком. Зависимость магнитной восприимчивости от температуры T таких парамагнетиков подчиняется закону Кюри – Вейсса: ,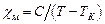

где С – константа, зависящая от рода вещества.

Для никеля температура Кюри равна 633 К (360°С), для железа - 770°С, для гадолиния - 17°С.

Согласно современным представлениям атомы, ферромагнетиков обладают большим магнитным моментом вследствие нескомпенсированности спиновых магнитных моментов части электронов. Из-за взаимного влияния магнитных моментов происходит их ориентировка независимо от внешнего магнит­ного поля, так что ферромагнетик на­магничен до насыщения уже без всякого поля. Наличие областей такого самопроизвольного намаг­ничивания (доменов) является наиболее характер­ным свойством ферромагнетиков. Существование доменов в ферромагнетиках доказано различными опытами, в том числе и прямыми наблюдениями. Типичная форма доменов при отсутствии внешнего поля показана на рис. 6.7. Стрелками указаны направления намагниченности насыщения в доменах. Размеры доменов обычно невелики – 0,1- 0,01 мм, поэтому усредненное даже по сравнительно небольшой области внутреннее поле равно нулю. Конфигурация направлений поля в соседних доменах, показанная на рис. 6.7 и 6.8а, когда поля в больших доменах как бы замыкаются полями малых концевых доменов, обеспечивает минимальное значение внутренней энергии ферромагнетика.

При вклю­чении внешнего поля энергии отдельных доменов делаются не­одинаковыми: энергия меньше для тех доменов, в которых намагниченность образует с направлением поля острый угол и больше в том случае, если этот угол ту­пой. Поэтому возникает процесс смещения границ доменов, при котором происходит рост доменов с меньшей энергией и уменьшение объема доменов с большей энергией. В случае очень слабых полей эти смещения границ обратимы и точно следуют за изменением поля. При увеличении поля смещения границ доменов делаются не­обратимыми (рис. 6.8б). При достаточной величине намагничивающего поля энергетически невыгодные домены исчезают вовсе (рис. 6.8в).

Если поле увеличивается еще больше, то возникает новый тип процесса намагничивания, при котором изменяется направление магнитного момента внутри домена (намагничивание вращения, рис. 6.8г). Наконец, в очень сильном поле магнитные моменты всех доменов устанавливаются параллельно полю. В этом состоянии ферромагнетик имеет наибольшую, возможную при данной темпера­туре намагниченность, т. е. намагничен до насыщения (рис. 6.8д).

а б в г д

Рис. 6.8. Процесс намагничивания ферромагнетика; а – внешнее поле В₀ отсутствует, д – поле максимально.

Указанные процессы намагничивания (за исключением смеще­ния границ в слабых полях) происходят с некоторой задержкой, т. е. смещение границ и поворот вектора намагниченности отстают от изменения поля, что приводит к появлению гистерезиса.

[1] Ферромагнетики с большой остаточной индукцией применяются как постоянные магниты.