Работа асинхронной машины с вращающимся ротором.

ЭДС и ток в обмотке ротора. Рассмотрим общий случай индуцирования ЭДС в обмотке ротора, увлекаемого вращающимся магнитным полем. Так как эта обмотка пересекается магнитным потоком с частотой пs = п1 - п2 , частота индуцируемой в ней ЭДС

(4.12)

f2 = pпs /60 = p(п1 — п2 )/60.

Учитывая, что pп1 /60 = f1 и (п1 - п2 )/п1 = s, представим (4.12) в ином виде:

(4.12a)

f2 = f1s.

При вращении ротора ЭДС в его обмотке

(4.13)

Е2s = 4,44f2 w2 kоб2 Фm = 4,44f1 sw2 kоб2 Фm.

Учитывая, что ЭДС при заторможенном роторе Е2 = 4,44f1 w2 kоб2 Фm, получаем

(4.13a)

Е2S = E2S .

Если обмотка ротора замкнута, по ней проходит ток с частотой f2 , который создает бегущую волну МДС F2 ; вращающуюся относительно ротора с частотой

nF2 = 60f2 /р = 60f1 s/p = n1s = n1 - п2 .

Направление вращения МДС ротора определяется порядком чередования максимумов тока в фазах, т. е. МДС ротора вращается в ту же сторону, что и магнитное поле статора (см. § 3.4). Легко заметить, что частота вращения МДС ротора относительно статора равна сумме частот п2 + nF2 = п1.

Следовательно, при вращении ротора МДС cтamopa F1 и МДС ротора F2 вращаются в пространстве с одинаковой частотой, т. е. относительно друг друга они неподвижны. Таким образом, полученные выше для заторможенного ротора выводы о взаимодействии токов в первичной и вторичной обмотках применимы и для вращающегося ротора.

Энергетическая диаграмма. При работе асинхронной машины в двигательном режиме (рис. 4.12) к статору из сети подводится мощность

(4.14)

P1 = m1 U1 I1 cos φ1 .

Часть этой мощности затрачивается на покрытие электрических потерь ΔРэл1 в активном сопротивлении обмотки статора и магнитных потерь ΔРм1 в статоре. В ротор посредством вращающегося магнитного поля передается электромагнитная мощность

(4.15)

Рэм = P1 - ΔРэл1 - ΔРм1 .

Часть электромагнитной мощности, полученной ротором, тратится на покрытие электрических потерь ΔРэл2 в его обмотке. В машинах с фазным ротором возникают также потери в щеточных контактах на кольцах, которые обычно включают в потери ΔРэл2. Оставшаяся часть мощности Рэм превращается в механическую мощность

(4.16)

Рмех = Рэм - ΔРэл2 .

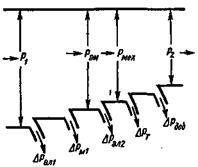Рис. 4.12.Энергетическая диаграмма асинхронной машины

Электромагнитный момент. Формулу (4.21), полученную из энергетической диаграммы, преобразуем к более удобному для анализа виду, подставив в нее значения

(4.27)

ω1 = 2πn1 /60 = 2π f1 /p;

(4.28)

ΔРэл2 = m2 I2 E2s cosψ2 ,

где ψ2 —угол сдвига фаз между ЭДС и током ротора.

При этом с учетом (4.13) получаем

(4.29)

М = (рт2 kоб2 /√2)Фm I2 cosψ2 = сM Фm I2 cosψ2,

где сM = рm2 kоб2 /√2 - постоянная.

Формула (4.29) справедлива не только для асинхронных машин, но и для электрических машин всех типов. Во всех этих машинах электромагнитный момент пропорционален произведению магнитного потока на активную составляющую тока ротора.