Переміщення точкових дефектів
Вакансії і міжвузольні атоми в твердому тілі при достатньо високій температурі Т рухливі. Для того, щоб переміститися із одного положення в інше, дефект повинен подолати потенціальний бар’єр. В любій кінетичній теорії допускається, що існують строго визначені стани для вихідної системи (атом поблизу вихідної точки) і для перехідної системи (атом біля сідлової точки). Це значить, що всі взаємодії, які відбуваються до розглядуваної частини фазового простору, досить малі.
У загальному випадку швидкість переміщення даного дефекту визначається виразом:
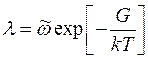 , (2.10.1)
, (2.10.1)
де G - вільна енергія, яка необхідна для перетворення дефекту із початкового рівноважного положення в сідлову точку; Т - абсолютна температура; k - постійна Больцмана; 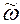 - ефективна частота коливань дефекту в напрямку сідлової точки. Хоча елементарним процесом є стрибок одного атома, розглядувана задача є по суті задачею багатьох тіл. Оскільки атом, який здійснює стрибок, оточений іншими атомами, з якими він взаємодіє. Виведення співвідношення (2.10.1) ґрунтується на статично-механічних уявленнях і якими тут нехтується (див. параграф 2.4).
- ефективна частота коливань дефекту в напрямку сідлової точки. Хоча елементарним процесом є стрибок одного атома, розглядувана задача є по суті задачею багатьох тіл. Оскільки атом, який здійснює стрибок, оточений іншими атомами, з якими він взаємодіє. Виведення співвідношення (2.10.1) ґрунтується на статично-механічних уявленнях і якими тут нехтується (див. параграф 2.4).
При виведені співвідношення (2.10.1) проблему дуже часто сильно спрощують, зводячи задачу багатьох тіл до одночасткової моделі. При такому підході 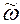 - не повністю визначена, або прирівнюється до енштейнівської частоти, а це допущення не повністю оправдане. Віннард узагальнив апарат статистичної механіки, розповсюдивши її на багаточастинкову модель.
- не повністю визначена, або прирівнюється до енштейнівської частоти, а це допущення не повністю оправдане. Віннард узагальнив апарат статистичної механіки, розповсюдивши її на багаточастинкову модель.
На рис.2.8 схематично показано N- мірні конфігураційний простір. Суцільні контурні лінії значать гіперповерхні постійної потенціальної енергії U. Точка А вказує на мінімум U, який відповідає атому гратки, сусідньому з вакансією, допускається, що всі інші атоми знаходяться в рівноважних умовах. Якщо цей атом помінявся місцями з вакансією і всі інші атоми з релаксували в свої вихідні положення, то мінімум потенціальної енергії знаходиться в точці В. Для того, щоб перейти з точки А в точку В, атом повинен подолати потенціальний бар’єр, проходячи через Р на рис.2.8. Гіперповерхня S є єдиною і проходить перпендикулярно контурів постійної U, через точку Р і значить розділяє області А і В.
Введемо поняття ефективної частоти,
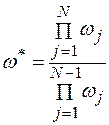 , (2.10.2)
, (2.10.2)
яка суттєво різниться від простої енштейнівської частоти або любої частоти в фізичному просторі Вона визначає собою добуток N частот нормальних коливань всієї системи у вихідній точці, поділеної на добуток N-1 частот нормальних коливань системи в конфігурації, яка відповідає сідловій точці. Введена нами ефективна частота 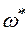 , зв’язана з
, зв’язана з 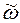 :
:
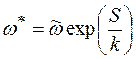 (2.10.3)
(2.10.3)
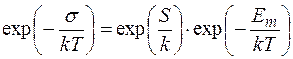 , (2.10.4)
, (2.10.4)
де Еm - енергія активації переміщення, яка рівна U(В) - U(А), що представляє собою роботу ,яку потрібно затратити, щоб ізотермічно перевести точку А в точку Р.
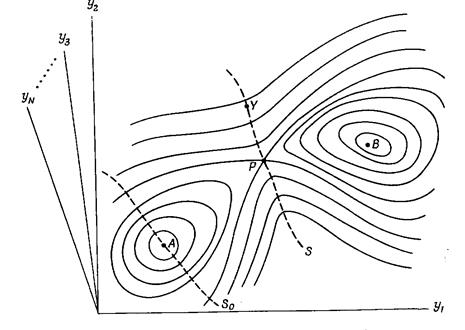
Рис.2.8. Схематичне зображення -N - мірного конфігураційного
простору з гіперповерхнями постійної потенціальної енергії
(суцільні лінії) і уявними обмежуючими гіперповерхні пунктирні лінії.
Точкою Р - позначена сідлова точка.
Вираз для швидкості стрибків (2.9.1) можна записати:
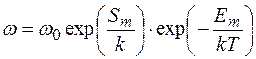 , (2.10.5)
, (2.10.5)
де 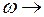 l в (2.10.1), а
l в (2.10.1), а 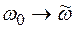 - ефективна частота коливань дефекту в напрямку сідлової точки, порядку 1013 сек-1.
- ефективна частота коливань дефекту в напрямку сідлової точки, порядку 1013 сек-1.
Отримане співвідношення (2.10.5) дозволяє встановити прямий зв’язок з теорією дифузії в твердих тілах. Якщо атом дифундує за рахунок переміщення вакансії, то ймовірність того, що він зміститься на одну міжатомну відстань рівна, ймовірності знаходження по сусідству з ним вакансії, помноженої на ймовірність того, що атом займе цю вакансію. Отже
J= 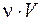 , (2.10.6)
, (2.10.6)
де V - концентрація вакансій в атомних долях. Комбінуючи (2.10.5) та (2.10.6) запишемо:
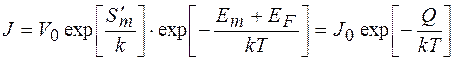 (2.10.7)
(2.10.7)
Звідси видно, що Q представляє собою суму енергій утворення і переміщення вакансії, а 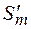 - суму відповідних ентропій. Вираз встановлює експоненціальний зв’язок швидкості з оберненою величиною абсолютної температури, часто називають рівнянням Авенаріуса. Можемо показати, що
- суму відповідних ентропій. Вираз встановлює експоненціальний зв’язок швидкості з оберненою величиною абсолютної температури, часто називають рівнянням Авенаріуса. Можемо показати, що
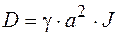 , (2.10.8)
, (2.10.8)
де 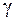 - геометрична константа; а - постійна гратки.
- геометрична константа; а - постійна гратки.
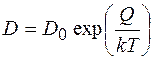 , (2.10.9)
, (2.10.9)
де Q - повна енергія активації самодифузії;
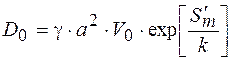 (2.10.10)
(2.10.10)
Ці формули справедливі для любого механізму дифузії.
Дата добавления: 2015-06-10; просмотров: 713;
