Погрешности измеренийи классы точности приборов
Одним из основополагающих понятий метрологии является понятие погрешности измерений.
Погрешностью измерения называют отклонение измеренного значения
физической величины от её истинного значения.
Погрешность измерений, в общем случае, может быть вызвана следующими причинами:
– несовершенством принципа действия и недостаточным качеством элементов используемого средства измерения;
– несовершенством метода измерений и влиянием используемого средства измерения на саму измеряемую величину, зависящим от способа использования данного средства измерения;
– субъективными ошибками экспериментатора.
Так как истинное значение измеряемой величины никогда неизвестно (в противном случае отпадает необходимость в проведении измерений), то численное значение погрешности измерений может быть найдено только приближенно. Наиболее близким к истинному значению измеряемой величины является значение, которое может быть получено при использовании эталонных средств измерений (средств измерений наивысшей точности). Это значение условились называть действительным значением измеряемой величины. Действительное значение также является неточным, однако, из-за малой погрешности эталонных средств измерений, погрешностью определения действительного значения пренебрегают.
1.5.1 Классификация погрешностей. По форме представления различают понятия абсолютной погрешности измерений и относительной погрешности измерений.
Абсолютной погрешностью измерений называют разность между измеренным и действительным значениями измеряемой величины:
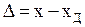 , (6)
, (6)
где ∆ – абсолютная погрешность,
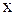 – измеренное значение,
– измеренное значение,
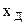 – действительное значение измеряемой величины.
– действительное значение измеряемой величины.
Абсолютная погрешность имеет размерность измеряемой величины. Знак абсолютной погрешности будет положительным, если измеренное значение больше действительного, и отрицательным в противном случае.
Относительной погрешностью называют отношение абсолютной погрешности к действительному значению измеряемой величины:
 (7)
(7)
где δ – относительная погрешность.
Относительная погрешность показывает, какую часть (в %) от измеренного значения составляет абсолютная погрешность. Относительная погрешность позволяет нагляднее, чем абсолютная погрешность, судить о точности измеренного значения.
1.5.2 Классы точности средств измерений. Исторически по точности средства измерений подразделяют на классы. Иногда их называют классами точности, иногда классами допуска, иногда просто классами.
Класс точности средства измерений – это его характеристика, отражающая точностные возможности средств измерений данного типа.
Допускается буквенное или числовое обозначение классов точности. Средствам измерений, предназначенным для измерения двух и более физических величин, допускается присваивать различные классы точности для каждой измеряемой величины. Средствам измерений с двумя или более переключаемыми диапазонами измерений также допускается присваивать два или более класса точности.
Если нормируется предел допускаемой абсолютной основной погрешности, или в различных поддиапазонах измерений установлены разные значения пределов допускаемой относительной основной погрешности, то, как правило, применяется буквенное обозначение классов.
Так, например платиновые термометры сопротивления изготовляют с классом допуска А или классом допуска В. При этом для класса А установлен предел допускаемой абсолютной основной погрешности:
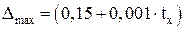 , (8)
, (8)
Соответственно, для класса B:
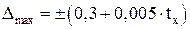 , (9)
, (9)
где 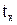 – температура измеряемой среды.
– температура измеряемой среды.
Если для средств измерений того или иного типа нормируется одно значение предельно-допустимой приведенной основной погрешности, или одно значение предельно-допустимой относительной основной погрешности, или указываются значения c и d, то для обозначения классов точности используются десятичные числа.
В соответствии с ГОСТом 8.401-80 для обозначения классов точности допускается применение следующих чисел:1∙10n; 1,5∙10n; 2∙10n; 2,5∙10n; 4∙10n; 5∙10n; 6∙10n, где n = 0, -1, -2, и т.д.
Для средств измерений с преобладающей аддитивной погрешностью численное значение класса точности выбирается из указанного ряда равным предельно-допустимому значению приведенной основной погрешности, выраженной в процентах.
1.5.3 Правила округления и записи результата измерений. Нормирование пределов допускаемых погрешностей средств измерений производится указанием значения погрешностей с одной или двумя значащими цифрами.
По этой причине при расчете значений погрешностей измерений также должны быть оставлены только первые одна или две значащие цифры.
Для округления используются следующие правила:
– погрешность результата измерения указывается двумя значащими цифрами, если первая из них не более 2, и одной цифрой, если первая из них 3 и более;
– показание прибора округляется до того же десятичного разряда, которым заканчивается округленное значение абсолютной погрешности;
– округление производится в окончательном ответе, промежуточные вычисления выполняют с одной – двумя избыточными цифрами.
Примеры округления и записи результата измерений с соблюдением обозначенных выше правил представлены в таблице 1.
Таблица 1 – Примеры округления и записи результата измерений
| Пример 1 | Показание прибора – 5,361 В; Вычисленное значение абсолютной погрешности – ± 0,264 В; Округленное значение абсолютной погрешности – ± 0,26 В; Результат измерения – (5,36 ± 0,26) В. |
| Пример 2 | Показание прибора – 35,67 мА; Вычисленное значение абсолютной погрешности – ± 0,541 мА; Округленное значение абсолютной погрешности – ± 0,5 мА; Результат измерений – (35,7 ± 0,5) мА. |
| Пример 3 | Вычисленное значение относительной погрешности – ± 1,268 %; Округленное значение относительной погрешности – ± 1,3 %. |
| Пример 4 | Вычисленное значение относительной погрешности – ± 0,367 %; Округленное значение относительной погрешности – ± 0,4 %. |
Дата добавления: 2015-06-05; просмотров: 1616;
