Лекция № 1
Основные свойства проецирования
Центральная проекция (перспектива).
Пусть дана некоторая плоскость П', которую называют плоскостью проекций, и вне ее точка S, называемая центром проекций.
Для построения изображения или проекции А' некоторой точки А проводят через точку А и центр проекций S прямую SA, называемую проецирующей прямой, а затем находят точку А' пересечения этой прямой с плоскостью П'.
Таков метод центрального проецирования точек пространстве на плоскость проекций П', его можно записать с помощью символов
А'=П' х SA
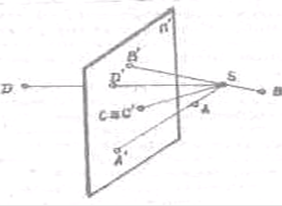 |
Проецирование можно выполнить для любой точки пространства, за исключением точек, лежащих в плоскости, проходящей через центр проекций S и параллельной плоскости проекций П'(Рис.1)
Рис.1.
Изображение предметов при помощи центрального проецирования обладает большой наглядностью, т.к. процесс человеческого зрения совпадает с операцией центрального проецирования.
Метод центрального проецирования сложен и в значительной степени искажает форму и размеры оригинала, т.к. не сохраняет параллельности прямых и отношения отрезков. Поэтому на практике пользуются методом параллельного проецирования ( в частности, ортогонального проецирования). Этот метод, является частным случаем центрального проецирования, когда центр проекций находится в бесконечно удаленной точке S¥ дает более простоепостроение изображения н в большей степени сохраняет те свойства оригинала, от которых зависят его форма н размеры.
Параллельная проекция
Пусть даны плоскость проекций П' и направление проецирования непараллельное плоскости проекций. Удалив центр проекций S¥ в бесконечно удаленную точку S¥, то все проецирующие прямые будут параллельны некоторому направлению S. Чтобы построить проекцию А' точки А, проводят проецирующую прямую параллельно направлению проецирования S, а затем находят точку А' пересечения прямой с плоскостью П' Таков метод параллельного проецирования точек пространства на плоскость проекций. (Pиc.2)
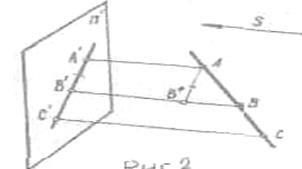
Рис.2.
Еще большее упрощение построения чертежа дает применение ортогонального проецирования, который является частным случаем параллельного перемещения, когда направление проецирования перпендикулярно плоскости проекции П'. В этом случае нетрудно установить соотношение между длиной натурального отрезка и длиной его проекции.
Ортогональная проекция получила наибольшее распространение в технических чертежах, т.к позволяет судить о размерах изображаемых предметов.
Рассмотренный метод проецирования позволяют однозначно решить прямую задачу, т.е. по данному оригиналу строить его проекционный чертеж. Обратная задача - по данному проекционному чертежу воспроизвести оригинал - не решается однозначно, т.е. чертеж не обладает свойством обратимости. Для получения обратимых чертежей дополняет проекционный чертеж необходимыми данными.
В данном курсе будут применяться два вида обратимых чертежей:
Комплексные чертежи в ортогональных проекциях и аксонометрические чертежи.
Рассмотрим некоторые свойства параллельной проекции.
1. Проекцией точки является точка.
2. Проекцией прямой линии является прямая линия.
3. Проекцией точки, лежащей на некоторой прямой, является точка, лежащая на проекции данной прямой, (свойство принадлежности).
4. Проекциями параллельных прямых являются параллельные прямые.
5. Отношения проекций отрезков, лежащих на параллельных прямых или на одной и той же прямой, равно отношению самих отрезков.
6. Проекция фигуры не меняется при параллельном переносе плоскости проекций,
Комплексный чертеж точки .
Чертеж, составленный из двух н более связанных между собой ортогональных проекций изображаемого оригинала, называется комплексным чертежом в ортогональных проекциях или комплексном чертежом. Принцип преобразования чертежа состоит в том, что данный оригинал проецируется ортогональна на две взаимно перпендикулярные плоскости проекций, которые затем совмещают с плоскостью чертежа.
Одна из плоскостей проекций П1 располагается горизонтально и называется горизонтальной плоскостью проекций, другая плоскость П2 располагается вертикально и называется фронтальной плоскостью проекций. Прямую пересечения плоскостей проекций называют осью проекций. В результате получаем две проекции горизонтальную проекцию точки а1 и фронтальную проекцию точки a2. (Рис.3)
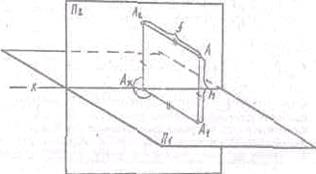
Рис.3.
Комплексный чертеж прямой
Прямая линия определяется двумя точками, поэтому на комплексном чертеже всякая прямая линия может быть задана проекциями A1A2 и B1B2 двух ее точек А и В. прямую на комплексном чертеже можно задать ее проекциями.
Прямая линия может занимать относительно плоскостей проекций различные положения
Комплексный чертеж называет эпюр Монжа или просто эпюр
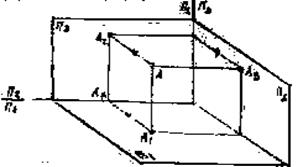
Рис.4.
Расстояние от точки А до плоскости П1 называют высотой точки (АА1). Расстояние от точки А до плоскости П2 называют глубиной точки (АА2). Расстояние о точки А до плоскости П3 называют шириной точки (АА3) (Рис. 4).На эпюре получен чертеж точки (Рис. 5).
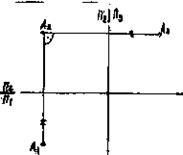
Рис.5
Плоскости проекций, пересекаясь, образуют оси координат, Точка пересечения координат, является началом координат. Любую точку пространства можно задать ее координатами. Рассмотрим построение точки по заданным координатам. (Рис.6).
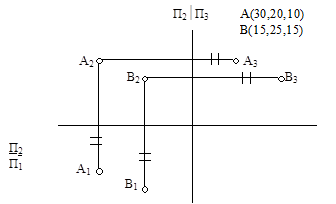 |
Рис.6.
| К ПРЕДЫДУЩЕЙ ЛЕКЦИИ | ОГЛАВЛЕНИЕ | К СЛЕДУЮЩЕЙ ЛЕКЦИИ |
| <== предыдущая лекция | | | следующая лекция ==> |
| Экспертиза промышленной безопасности | | | Определение истинной ( натуральной) величины отрезка прямой |
Дата добавления: 2015-06-05; просмотров: 993;
