Электрическое поле при наличии диэлектриков.
Диэлектрики делятся на два типа: полярные и неполярные. Неполярный диэлектрик при  имеет дипольный момент молекулы, равный нулю
имеет дипольный момент молекулы, равный нулю 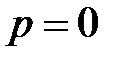 . К ним относятся молекулы:
. К ним относятся молекулы: 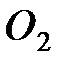 и
и 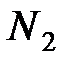 .
.
Полярные диэлектрики при  имеют отличный от нуля дипольный момент:
имеют отличный от нуля дипольный момент: 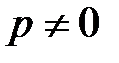 .
. 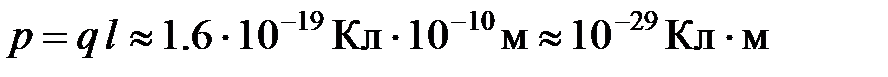 Пример:
Пример: 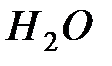 .
.
В присутствии электрического поля в неполярных диэлектриках возникает дипольный момент:
 , (2.18)
, (2.18)
где 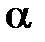 – молекулярная восприимчивость. У неполярных и полярных диэлектриков при
– молекулярная восприимчивость. У неполярных и полярных диэлектриков при 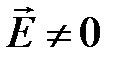 происходит ориентация
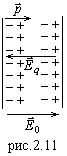
происходит ориентация 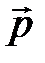 вдоль поля. Этот процесс называется поляризацией. Как видно из рис.2.11, внутри диэлектрика соседние разноименные заряды диполей компенсируются. Не скомпенсированы лишь диполи на поверхности диэлектрика. Видно, что внутри возникло поле
вдоль поля. Этот процесс называется поляризацией. Как видно из рис.2.11, внутри диэлектрика соседние разноименные заряды диполей компенсируются. Не скомпенсированы лишь диполи на поверхности диэлектрика. Видно, что внутри возникло поле 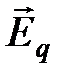 , антипараллельное внешнему полю
, антипараллельное внешнему полю 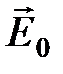 :
: 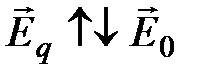 ,
, 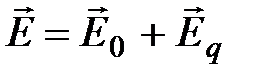 ;
; 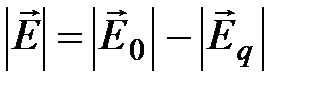 - т.е. поле внутри диэлектрика меньше внешнего.
- т.е. поле внутри диэлектрика меньше внешнего.
Общая поляризованность – это суммарный дипольный момент единицы объема диэлектрика:
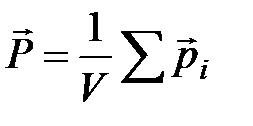 ;
;
Размерность 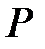 - Кл/м2. Величина
- Кл/м2. Величина 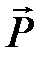 зависит от
зависит от 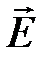 линейно:
линейно:
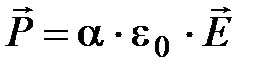 , (2.19)
, (2.19)
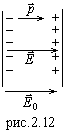
где 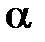 - диэлектрическая восприимчивость единицы объема. Взаимная ориентация векторов
- диэлектрическая восприимчивость единицы объема. Взаимная ориентация векторов 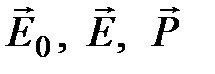 показаны на рис.2.11 и 2.12.
показаны на рис.2.11 и 2.12.
Теорема Гаусса для вектора поляризованности.
Поляризованность 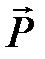 создается связанными зарядами внутри диэлектрика. Чтобы найти величину этих зарядов, рассмотрим вывод теоремы Гаусса для
создается связанными зарядами внутри диэлектрика. Чтобы найти величину этих зарядов, рассмотрим вывод теоремы Гаусса для 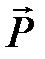 .
.
Произвольная замкнутая поверхность 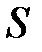 (рис.2.13) охватывает часть объема внутри диэлектрика. На рис.2.13 изображена лишь часть этой поверхности. При включении внешнего поля диэлектрик поляризуется: положительные заряды смещаются вдоль поля, отрицательные – против.
(рис.2.13) охватывает часть объема внутри диэлектрика. На рис.2.13 изображена лишь часть этой поверхности. При включении внешнего поля диэлектрик поляризуется: положительные заряды смещаются вдоль поля, отрицательные – против.
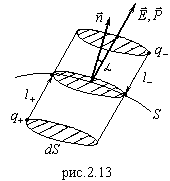 Возьмем элемент поверхности
Возьмем элемент поверхности 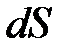 . Найдем заряд, пересекающий
. Найдем заряд, пересекающий 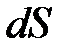 под действием поля. Пусть положительный заряд смещается на
под действием поля. Пусть положительный заряд смещается на 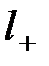 , а отрицательный – на
, а отрицательный – на 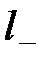 . Плотность этих зарядов -
. Плотность этих зарядов - 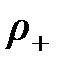 и
и 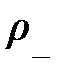 . Тогда, построив на
. Тогда, построив на 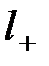 ,
, 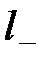 и
и 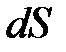 косой цилиндр, рассчитаем общий положительный и отрицательный заряды, прошедшие через
косой цилиндр, рассчитаем общий положительный и отрицательный заряды, прошедшие через 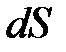 .
.
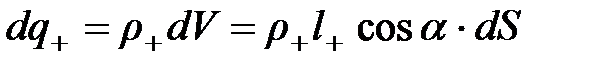 ,
,
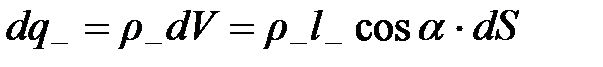
здесь 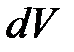 - объемы соответствующих частей цилиндра.
- объемы соответствующих частей цилиндра.
Суммарный заряд, прошедший через 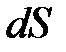 :
:
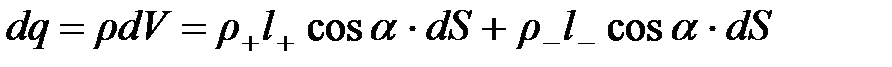 ,
,
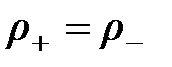 ,
, 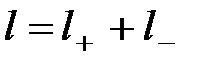 -расстояние, на которое сместились заряды. Тогда:
-расстояние, на которое сместились заряды. Тогда:
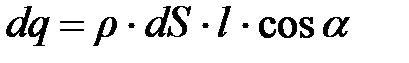 , (2.20)
, (2.20)
Так как:
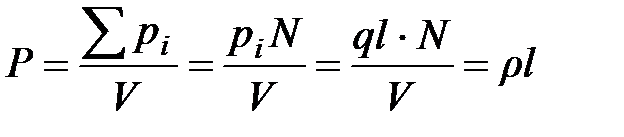 , (2.21)
, (2.21)
где соотношение 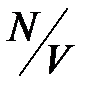 представляет собой концентрацию диполей (связанных зарядов). Поэтому, подставив (2.20) в (2.19), получим:
представляет собой концентрацию диполей (связанных зарядов). Поэтому, подставив (2.20) в (2.19), получим:
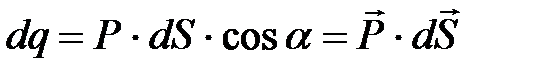 . (2.22)
. (2.22)
Проинтегрировав выражение (2.22) по всей замкнутой поверхности 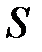 , находим весь заряд, пересекший поверхность
, находим весь заряд, пересекший поверхность 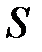 :
:
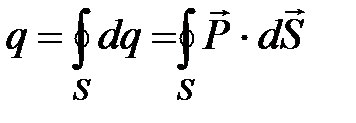 .
.
В результате выхода из поверхности положительных зарядов и входа в поверхность отрицательных зарядов внутри поверхности появляется не скомпенсированный заряд (при 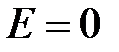 внутри поверхности число положительных и отрицательных зарядов было одинаковым, диэлектрик электрически нейтрален). При этом возникает связанный заряд, отрицательный по величине:
внутри поверхности число положительных и отрицательных зарядов было одинаковым, диэлектрик электрически нейтрален). При этом возникает связанный заряд, отрицательный по величине:
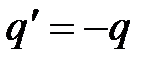 .
.
Тогда внутри поверхности появляется избыточный отрицательный заряд:
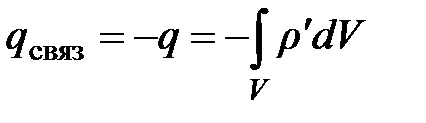 , (2.22’)
, (2.22’)
где 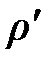 - плотность связанных зарядов внутри
- плотность связанных зарядов внутри 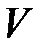 :
:
 . (2.23)
. (2.23)
Это теорема Гаусса для вектора поляризованности 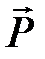 :
:
поток вектора поляризованности сквозь замкную поверхность равен отрицательному связанному заряду, возникающему внутри поверхности
Дата добавления: 2015-06-01; просмотров: 987;
