Разделение контуров
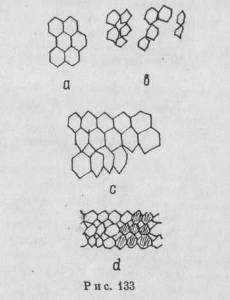
Плоскость b и изображение а на рис. 129 имеют общую пограничную линию. Установление границ — сама по себе трудная задача. На рис. 131 изображены два шестиугольника, которые стремятся отделиться друг от друга. При более специфических условиях можно действительно видеть такое отделение одной фигуры от другой. Если в течение долей секунды предъявлять расплывчатые фигуры, то управление восприятием со стороны коры головного мозга ослабевает. В результате модель, наподобие той, которая показана на рис. 132, а, иногда воспроизводится испытуемым в виде рис. 132, b, что свидетельствует о стремлении наделить каждую изобразительную единицу своим собственным контуром. В одном из экспериментов Пиаже попросил маленьких ребятишек срисовать композиции из геометрических фигур, в которых окружности или треугольники касались друг друга. В своих рисунках дети, как правило, изображали эти фигуры разобщенными. В усовершенствованном Гансом Раппом тесте для определения художественных способностей человека испытуемых просили нарисовать модель, напоминающую по своему внешнему виду восковые пчелиные соты (рис. 133,а). Чаще всего при этом изображались самостоятельные, независимые друг от друга шестиугольники и между ними оставлялось

пустое пространство, а некоторые из испытуемых даже подчеркивали получающиеся промежутки посредством нанесения теней. В других случаях испытуемые вводили оверлэппинг, который разрушал форму одной из фигур, с тем чтобы освободить ее соседку (рис. 133, b, d,c).
В приведенных нами примерах составные части контура выступают в роли равных партнеров, ни один из которых не претендует на привилегированное положение. Другой смысл носит изображение на рис. 129. В этом примере изображение а представляет собой компактную фигуру, которая обладает простым очертанием, ограничивающим площадь сравнительно высокой плотности, тогда как плоскость b воспринимается как бесконечная и рыхлая субстанция. При таких условиях неопределенность общей границы может быть устранена. Фигура, имеющая форму круга, обладает достаточной силой, чтобы вырвать границу из плоскости b и монополизировать ее как свой собственный контур. Очертание этой фигуры воспринимается принадлежащим фигуре а, но не плоскости b.
При восприятии плоскости b зритель находится в затруднительном положении, так как эта плоскость оканчивается там, где начинается изображение а, но не имеет собственной границы. Возникает визуальный парадокс. Удовлетворительное разрешение этого парадокса будет в том случае, если плоскость b представить как непрерывную поверхность, лежащую под фигурой а. В этом случае
потребность в пограничной линии отпадает. Данный анализ показывает, что разделение модели на два уровня служит двойной цели. Оно позволяет избежать разрыва во внешней поверхности и упразднить дилемму ее окончания, когда поверхность не имеет конца.
Неопределенность общего контура усугубляется тем, что хотя физически контур остается неизменным и постоянным, тем не менее кажется, что он имеет различный внешний облик в зависимости от того, воспринимается ли он принадлежащим той или другой из примыкающих поверхностей. Например, линия на рис. 129 кажется

выпуклой по отношению к внутренней поверхности и вогнутой по отношению к внешней. Эти два варианта формы объекта являются несовместимыми, потому что предмет не может восприниматься в одно и то же время и как выпуклый, и как вогнутый.
Пример, приведенный на рис. 134, взят из картины Брака. Форма линии профиля целиком изменяется в зависимости от того, к какому лицу при восприятии данного рисунка мы ее относим. То, что было пустым, становится наполненным, то, что являлось активным, становится пассивным. Примеры такого рода можно обнаружить повсюду. Некоторые художники-сюрреалисты (такие, например, как Дали) использовали технические приемы, с тем чтобы вызвать известные трюки при игре в прятки, с помощью которых на картине можно было изобразить различные, взаимно исключающие объекты. Эти композиции предназначались для того, чтобы шокировать зрителя с его благодушной верой в реальную действительность.
Дата добавления: 2015-06-01; просмотров: 814;
