Современная (текущая) величина аннуитета
Помимо наращенной суммы обобщающей характеристикой потока платежей является современная величина. Современная (текущая) величина потока платежей (капитализированная или приведенная величина) – это сумма платежей, дисконтированных на момент начала ренты по ставке начисляемых сложных процентов. Это важнейшая характеристика финансового анализа, т.к. является основой для измерения эффективности различных финансово-кредитных операций, сравнения условий контрактов и т.п. Данная характеристика показывает, какую сумму следовало бы иметь первоначально, чтобы, разбив ее на равные взносы, на которые начислялись бы установленные проценты в течение всего срока, можно было бы получить указанную наращенную сумму.
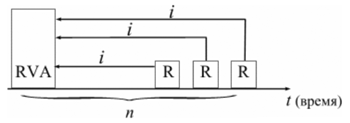
|
| Рис. 8. Логика финансовой операции определения современной величины потока платежей. |
В этом случае реализуется схема дисконтирования: все элементы с помощью дисконтных множителей приведены к одному моменту времени, что позволяет их суммировать.
В простейшем случае, для годовой обычной ренты с выплатами в конце каждого года, когда момент оценки совпадает с началом ренты, современная величина финансовой ренты равна:
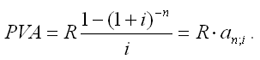
|
Дробь в формуле – коэффициент приведения ренты (an ; i), значения которого табулированы для широкого круга значений, поскольку зависят от ставки процентов (i) и от числа лет (n) (Приложение 5).
Пример. Определить по данным примера современную величину ренты.
Решение:
Современная величина ренты составит:

|
Таким образом, все производимые в будущем платежи оцениваются в настоящий момент в размере 1'217,78 руб.
Рассмотрим расчет современной величины ренты для различных ее видов:
- годовая рента с начислением процентов несколько раз в год

|
- срочная рента при начислении процентов один раз в год
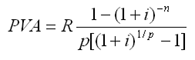
|
- срочная рента с неоднократным начислением процентов в течение года, при условии, что число выплат не равно числе начислений, т.е. p ≠ m.
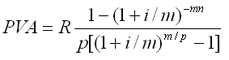
|
Дата добавления: 2015-05-28; просмотров: 1071;
