АБСОЛЮТНАЯ ПРОНИЦАЕМОСТЬ
6.2.1. ПРОНИЦАЕМОСТЬ ПОРОД С МЕЖЗЕРНОВОЙ ПОРИСТОСТЬЮ (УРАВНЕНИЕ КОЗЕНИ — КАРМАНА)
Представим себе пористую среду в виде цилиндра сечением to и длиной ∆L, внутри которого расположен извилистый цилиндрический канал длиной ∆LK со среднестатическим сечением ωк. Отношение ωк/ω = φ представляет собой среднестатистическую просветность породы в любом сечении образца, перпендикулярном к среднему направлению потока (рис. 24).
Линейную скорость истечения флюида через такой канал υH можно определить по закону Пуазейля:
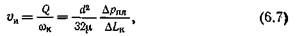
где Q — расход жидкости; d — диаметр канала; µ — вязкость жидкости.
| 1 Часто для этой цели на практике используют проницаемость, определенную при минерализованной воде. |
Используем понятие о гидравлическом радиусе канала про
извольного сечения (Блейк, 1921 г.): •
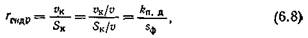
где vK, v — объемы фильтрующих каналов и образца; SK — по-верхность фильтрующих каналов; kn.a — коэффициент динамической пористости; 5ф — удельная поверхность фильтрующих каналов.
В частном случае капилляра круглого сечения
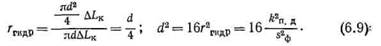
С учетом изложенного, уравнение (6.7) для линейной скорости истечения флюида через цилиндрический канал можно представить:
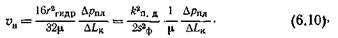
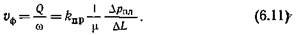
|
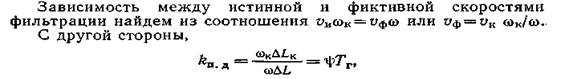
|
В то же время линейную скорость фильтрации, полученную путем отнесения расхода флюида к сечению всего образца, можно определить из уравнения Дарси:
где Тг — гидравлическая извилистость каналов; я|з — просвет-ность пористой среды.

|
| Подставив (6.12) в уравнение (6.11), получим: |
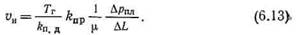
|
| Приравняем левые части уравнений (6.10) и (6.13): |
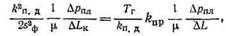
|
| откуда найдем выражение для проницаемости: |

|
Из двух последних равенств можно получить
Это уравнение Козени — Кармана для модели пористой среды с капиллярами круглого сечения (цифра «2» в знаменате-
ле — коэффициент формы сечения круглого капилляра). П.Карман на основе решения уравнений Навье — Стокса нашел, что для круглого, эллиптического, квадратного, треугольного, прямоугольного, щелевого с коаксиальными стенками сечений каналов величина постоянного коэффициента изменяется от 2 до 3. Среднее значение 2,5. Обозначим этот коэффициент через f. Тогда уравнение (6.14) для каналов любого сечения примет вид:

Экспериментальная проверка уравнения Козени—Кармана была произведена многими авторами на самых разных моделях неконсолидированных пористых сред. Проверка показала, что если удельную поверхность фильтрации этих моделей вычислять как сумму поверхностей отдельных фракций частиц и размеры частиц в крайних фракциях не отличаются более чем в 5 раз, то уравнение (6.15) хорошо описывает связь между проницаемостью, пористостью и удельной поверхностью неконсолидированных пористых сред.
Уравнение (6.15), кроме того, объясняет существование целой группы петрофизических связей для консолидированных пород с использованием коэффициента проницаемости.
1. Для сцементированных литологически однородных и одновозрастных песчано-алевритовых слабоглинистых пород, в которых коэффициенты пористости и удельной поверхности меняются сравнительно мало (kп.д≈const и sф≈const), а величина проницаемости обусловлена переотложением вторичного цементирующего материала, изменяющим извилистость каналов, уравнение (6.15) принимает вид
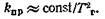
Зависимости такого рода получены О. А. Черниковым и А. И. Куренковым (1962) для песчаников: XVII горизонта Узенского месторождения, пласта C1 Мухановского месторождения и пласта Д1 Туймазинского месторождения [1] и М. М. Элланским для песчаных коллекторов Калужского подземного хранилища газа.
2. Для слабоуплотненных карбонатных пород с межкристаллической и межзерновой пористостью удельная поверхность и извилистость изменяются в узких пределах (sф≈const), а извилистость в результате слабого уплотнения имеет небольшое значение, которое также можно принять в первом приближении равным Тг ≈const.
Наиболее сильным фактором, влияющим на проницаемость, в этом случае будет пористость в третьей степени:
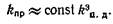
На рис. 25 приведена эта приближенная зависимость.
3. Для пористых карбонатных пород содержание остаточной воды kв.о в зоне предельного нефтенасыщения может быть определено с помощью введения понятия о средней толщине-пленки связанной воды и воды углов пор в гидрофильных породах τср:
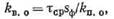
откуда
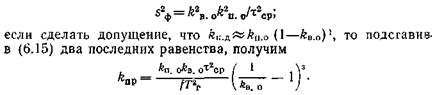
При kв.о→1, kпр→0 — тонкозернистые низкопористые и малопроницаемые известняки, а при kB→0, kпр→∞ — высокопроницаемые известняки с повышенной пористостью.
Поскольку для карбонатных пород в первом приближении, можно принять kп.оkв.о≈const и (τср/Iг)2≈const, предыдущее равенство можно записать так:
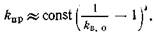
На рис. 26 приведены зависимости, удовлетворяющие полученному уравнению.
4. Из уравнения (6.15) найдем:
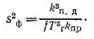
Это — возможное уравнение для определения удельной поверхности фильтрации.
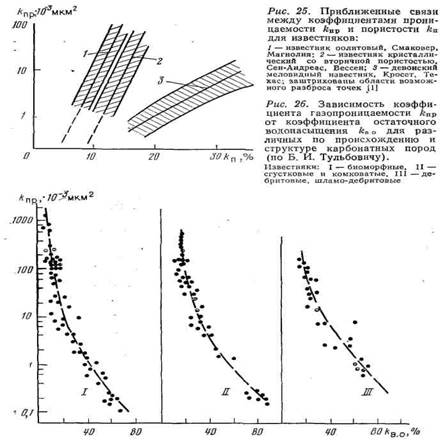
В двойном логарифмическом масштабе уравнение
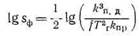
представляет собой прямую с угловым коэффициентом tgά=2. Проверка этого выражения выполнена многими исследователями. Оно дает возможность выйти на определение фильтрационной неоднородности пород по данным геофизических исследований скважин.
|
«.2.2. ПРОНИЦАЕМОСТЬ ТРЕЩИНОВАТЫХ ПОРОД
Расход жидкости Q через прямоугольную щель с раскрытием (высотой) b и шириной а можно установить из известного уравнения Буссинска (в оригинале все размерности в СГС):

откуда можно найти линейную скорость истечения жидкости υн, отнеся расход к площади трещины ωT = ab:
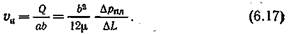
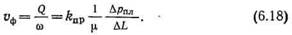
|
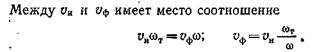
|
Если, как в пористой среде, расход отнести не к площади трещины, а ко всей площади фильтрующей среды ω, то согласно уравнению Дарси
Отношение ωт/ω есть просветность трещинной среды в направлении фильтрации. Если трещины в породе располагаются в одном направлении, то просветность равна коэффициенту трещиноватости в направлении фильтрации kт= ωт/ω.
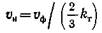
|
| и уравнение (6.17) примет вид |
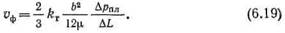
|
При равномерной системе трещин в трех взаимно перпендикулярных направлениях просветность среды в направлении фильтрации равна ωт/ω = 2/зkт. Для этого случая
Приравнивая левые части уравнений (6.18) и (6.19) и разрешая это равенство относительно kпр, получим для равномерной системы трещин в трех взаимно перпендикулярных направлениях:

И для двух систем взаимно перпендикулярных трещин, параллельных направлению фильтрации

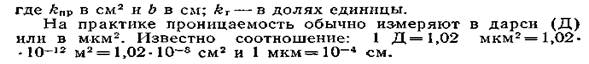
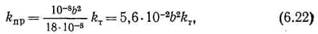
|
| и для системы трещин одного или двух параллельных направлений |
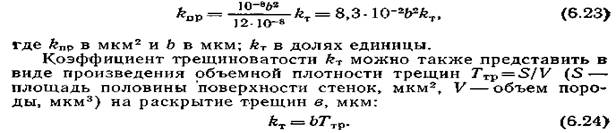
|
| Тогда, например, для случая системы трещин трех направлений уравнение (6.22) примет вид |

|
. С учетом последних равенств уравнение (6.20) для системы трещин в трех взаимно перпендикулярных направлениях примет вид
При определении трещиноватости пород в крупных плоскопараллельных шлифах (Е. С. Ромм, Л. П. Гмид) это уравнение можно использовать для приближенной оценки проницаемости. Все величины, входящие в уравнение, можно определить визуально.
Если принять, что наиболее часто встречающаяся величина раскрытости микротрещин в шлифах уплотненных карбонатных пород составляет b≈15 мкм, то получится приближенная связь проницаемости микротрещиноватых пород с коэффициентом трещиноватости:
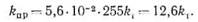
Коэффициент трещиноватости карбонатных пород при определениях на кернах пород редко превышает величину kт = 0,3% (Л. П. Гмид). Это означает, что проницаемость микротрещиноватых разностей не должна быть выше
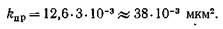
Коэффициент трещиноватости, установленный по длине микротрещин в шлифе, характеризует не всю полезную емкость, включающую каверны, расширения, отдельные поры, а лишь объем микротрещин в шлифе. Однако величина kT определяет фильтрационные свойства микротрещиноватых пород. Уменьшение коэффициента трещиноватости до значения kт<1,0-10-4
(0,01%) снижает проницаемость породы до величины kпр≤1х10-3 мкм2. Такая порода уже перестает быть коллектором.
Если представить себе трещинную среду в виде системы бесконечных прямых трещин трех взаимно перпендикулярных направлений, с раскрытием b и расстоянием между трещинами а,
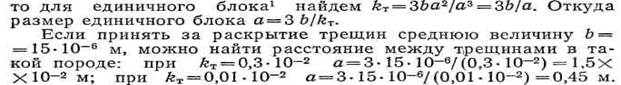
Другими словами, при kт = 0,3% расстояние между трещинами составляет около 1 см и можно еще наблюдать эту трещиноватость на больших кернах или в шлифах размером около 10 см.
Очевидно, что при более высокой равномерной трещиноватости или при большем раскрытии трещин порода, скорее всего, не сохранит свою сплошность — керн разрушится при его отборе. По крайней мере, вероятность отбора керна с более высокой равномерной трещиноватостью снижается. Керн из высокопродуктивных пластов, проницаемость которых обеспечивается более высокой раскрытостью трещин, также, как правило, не выносится или выносится практически непроницаемая матрица.
Изучение по кернам или шлифам пород с равномерной открытой трещиноватостью и с низким коэффициентом kт<0,01%, по-видимому, также затруднено, так как для этого понадобилось бы иметь образцы нереально больших размеров. Эти примеры показывают, что в связи с недостаточной представительностью отдельно взятых кернов трещиноватых пород, для достоверного изучения их проницаемости в широком диапазоне изменения трещивоватости необходимо использовать коллекции кернов при условии его сплошного отбора в базовых скважинах или применять другие методы, обеспечивающие исследования больших объемов пород, например, гидродинамические и геофизические.
Дата добавления: 2015-05-26; просмотров: 4592;
