Эффект Комптона

При большой энергии фотонов, в частности, для рентгеновского излучения ( 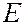~ 0,1 МэВ) процесс поглощения фотонов электронами вещества становится маловероятным. В этом случае при взаимодействии электромагнитного излучения с веществом наблюдается его рассеяние с изменением направления распространения.

В 1923 г. А.Комптон, изучая рассеяние рентгеновского излучения на парафине, обнаружил, что длина волны рассеянного излучения 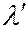больше, чем длина волны 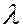падающего излучения. Такой эффект увеличения длины волны излучения вследствие рассеяния его веществом получил название эффекта Комптона. Открытие и объяснение этого эффекта квантовой оптики в 1927 г. было удостоено Нобелевской премии по физике.

Схематически экспериментальная установка Комптона изображена на рисунке. Рентгеновская трубка РТ была смонтирована на вращающейся платформе, что позволяло при ее повороте изменять угол рассеяния 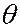рентгеновского излучения, попадающего после мишени-рассеивателя 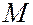в измерительный блок установки. Длина волны 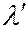рассеянного излучения определялась с помощью дифракции его на кристалле. Согласно дифракционной теории при выполнении условия Вульфа-Брегга

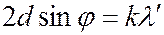
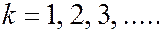(6.41.12)

где 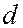- расстояние между атомными плоскостями кристалла, а 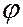- угол скольжения падающего излучения, наблюдается интенсивное отражение от кристалла рассеянного рентгеновского излучения. Поэтому, зная параметры кристаллической решетки 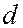и измерив угол 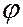для максимума отражения 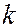-ого порядка, можно рассчитывать длину волны 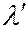рентгеновского излучения, рассеянного мишенью .

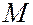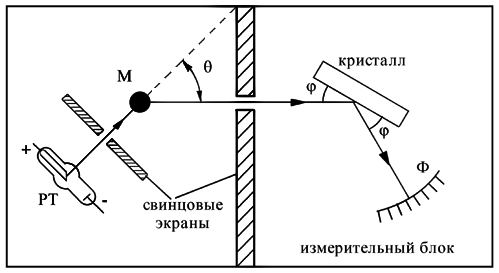
Схема установки для изучения эффекта Комптона

Как установил экспериментально Комптон, длина волны рассеянного излучения оказалась больше длины волны падающего излучения, причем изменение длины волны не зависело от материала рассеивателя, а определялось только величиной угла рассеяния 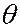. Опытным путем Комптон показал, что 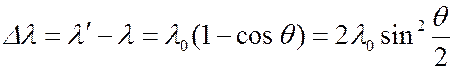(6.41.13)

Это соотношение называют формулой Комптона. Значение постоянной 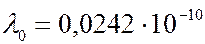м Комптон определил экспериментально.

Эффект Комптона относится к явлениям квантовой оптики, и фотонная теория излучения объясняет этот эффект как следствие упругого рассеяния фотона на свободном электроне вещества. Формула Комптона (6.41.13) при этом оказывается следствием законов сохранения энергии и импульса в упругом соударении фотона и электрона.

Действительно, в системе отсчета, в которой свободный электрон первоначально покоился, закон сохранения энергии с учетом возможных релятивистских скоростей электрона после удара может быть записан в виде

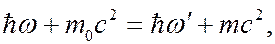(6.41.14)

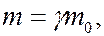
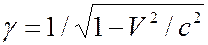где – масса покоя электрона, – релятивистский множитель, – скорость электрона после столкновения с фотоном, – частота падающего излучения, 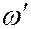– частота рассеянного излучения.

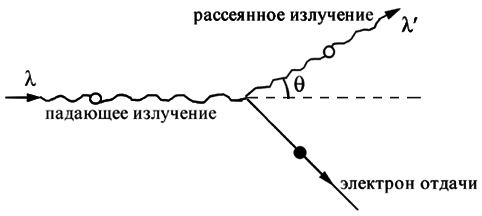
Рассеяние фотона на свободном электроне

Разделив члены уравнения (1.60) на 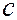, его можно преобразовать к виду

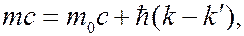(6.41.15)

где , .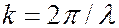

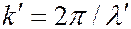Заметим, что уже закон сохранения энергии (6.41.14) объясняет эффект Комптона качественно. Действительно, так как 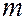> , то из (6.41.14) следует, что > ( < ) .

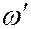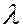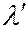Возведем левую и правую части уравнения (6.41.15) в квадрат:

(6.41.16)

В упругом столкновении фотона с электроном выполняется также закон сохранения импульса, который можно записать в виде

(6.41.17)

Построив векторную диаграмму закона сохранения импульса, из треугольника импульсов находим, что

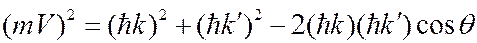, (6.41.18)

где 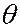– угол между направлениями падающего и рассеянного излучения.

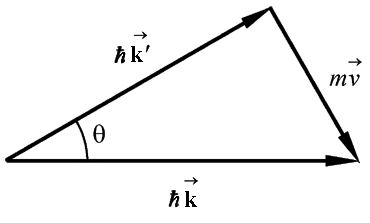
Треугольник импульсов

Вычтем из (6.41.16) выражение (6.41.18):

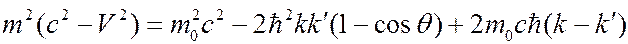(6.41.19)

Выражение (6.41.19) можно преобразовать к виду:

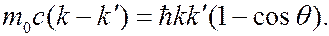(6.41.20)

Умножив члены равенства (6.41.20) на 2 и разделив на 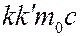, получим:

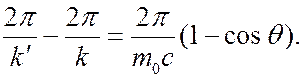(6.41.21)

Так как 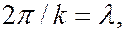окончательно получаем формулу Комптона:

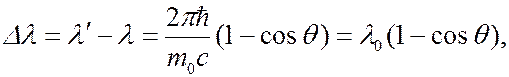(6.41.22)

где

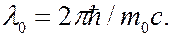(6.41.23)

Величину

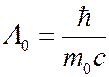(6.41.24)

называют комптоновской длиной волны частицы, масса покоя которой равна . Комптоновская длина волны электрона 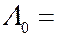3,86∙10^{-13 м.}

Сравнение (6.41.22) с (6.41.13) показывает прекрасное совпадение выводов квантовой теории излучения и эксперимента. Из этих формул следует, что максимальное изменение длины волны излучения наблюдается для угла рассеяния , и оно равно 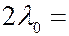4,84∙10^{-12 м}. В силу малости

значения практически изменение длины волны при рассеянии на свободных электронах можно обнаружить лишь в экспериментах с коротковолновыми рентгеновским или гамма излучениями.

Следует заметить, что значительная часть электронов вещества не является свободными, а связаны с атомами. Если энергия кванта излучения велика по сравнению с энергией связи электрона, то рассеяние на таком электроне происходит как на свободном электроне. В противном случае, рассеиваясь на связанном электроне, фотон обменивается энергией и импульсом фактически со всем атомом в целом. При таком рассеянии для расчета изменения длины волны излучения также можно применить формулу (6.41.22), где, однако, под следует понимать уже массу всего атома. Это изменение оказывается настолько малым, что его нельзя практически обнаружить экспериментально.

В диапазоне энергий квантов 0,1− 10 МэВ комптон-эффект является основным физическим механизмом энергетических потерь 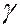-излучения при его распространении в веществе. Поэтому комптоновское рассеяние широко используется в исследованиях 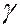-излучения атомных ядер. Оно лежит в основе принципа действия некоторых гамма-спектрометров.

Контрольные вопросы для самоподготовки студентов:

1. Внешний фотоэффект и его законы.

2. Уравнение Эйнштейна для внешнего фотоэффекта.

3. Что такое фотон? Масса и импульс фотона. Давление света.

4. Внутренний фотоэффект.

5. Вентильный фотоэффект.

6. Корпускулярно-волновой дуализм света.

7. Эффект Комптона.

Литературные источники

1. Трофимова, Т.И. Курс физики: учеб. пособие для вузов / Т.И. Трофимова. – М.: ACADEMIA, 2008.

2. Савельев, И.В. Курс общей физики: учеб. пособие для втузов: в 3-х томах / И.В.Савельев. – СПб.: Спец. лит., 2005.