Область пространства, существенно участвующая в формировании поля на заданной линии радиосвязи

В теории распространения радиоволн, особенно при оценке вли­яния земли, важное значение имеет понятие «существенная область». Наличие существенной области можно определить путем эксперимента. Установим на пути распространения волны от точки А к точке В непрозрачный для радиоволн экран с отвер­стием переменного диаметра d (рисунок 3). Если диаметр отверстия велик, что соответ­ствует отсутствию экрана, напряженность поля в точке В равна величине Е₀.

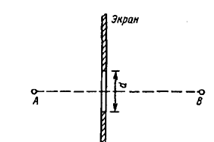
Рисунок 3. Непрозрачный для радиоволн экран с отвер­стием переменного диаметра

Будем затем уменьшать диаметр отверстия до тех пор, пока измерительный прибор не покажет явного уменьшения поля. Соответ­ствующее значение d и есть диаметр облас­ти, существенно участвующей в передаче энергии волны. Помещая экран на разных расстояниях от источника, можно таким образом выявить конфигурацию существенной области.

Форму и размеры существенной области возможно установить и аналитически, используя принцип эквивалентности. Согласно этому принципу поле в точке приема определяется суммарным дей­ствием вторичных источников, распределенных по воображаемой по­верхности, замкнутой вокруг источника А или точки приема В.

Выберем поверхность, которая охватывает источник, и для уп­рощения расчетов составим ее из бесконечной плоскости S₀, располо­женной перпендикулярно линии АВ (рисунок 4), и полусферы S_∞ с бесконеч­ным радиусом, которая замыкает плос­кость S.

Поля от источников, расположен­ных на бесконечно удаленных участках поверхности 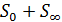,бесконечно малы вследствие расходимости волны. Поэто­му суммарное поле формируется источниками на поверхности S₀, распо­ложенными на конечном расстоянии от точки В. Для облегчения суммирования разделим плоскость S₀ на зоны Френеля.

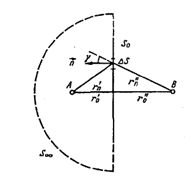
Рисунок 4. Пояснения к определению существенной области

Построим серию ломаных АС_nВ (рисунок 5, а), пересекающих плоскость S₀так, чтобы длина каждой последующей ломаной была больше длины предыдущей на половину длины волны:

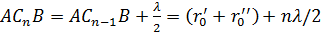(13)

Семейство ломаных линий, удовлетворяющих условиям (13), при пересечении с плоскостью S₀ образует на этой плоскости систему окружностей с центром в точке 0 (рисунок 5, б). Участки плоскости, ограниченные окружностями, называют зонами Френеля на плоскости. Первая зона представляет собой круг, зоны высших номеров - кольце­вые области. Суммарное поле от всех источников рассчитывается с учетом их распределения по зонам Френеля. Амплитуда поля от элемента поверх­ности ΔS оценивается как 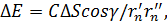а фаза определяется 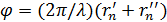где С - константа, зависящая от свойств первичного источника; обо­значения γ, r'_n, r''_n приведены на рисунке 4.

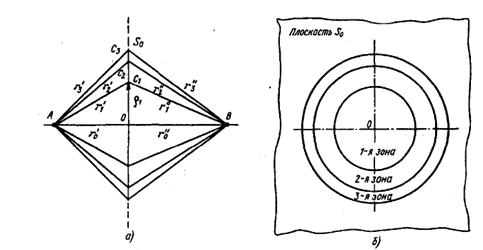
Рисунок 5. Зоны Френеля

На рисунке 6 показано векторное суммирование элементарных составляющих ΔЕ, возбужденных источниками двух зон с номерами п и п + 1.

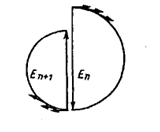
Рисунок 6. Векторное суммирование элементарных составляющих ΔЕ

Расчеты показывают, что результирующие векторы полей от источников соседних зон почти коллинеарны, при этом векторы 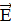_п и 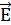_n+i (рисунок 6) направлены противоположно из-за различия на λ/2 длин путе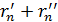й и 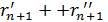согласно (13). Амплитуда E_(n+1)mах << E_nmах поскольку путь 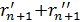> 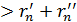и с увеличением п умень­шается значение cos γ. B результате коллинеарности векторов полей от источников в отдельных зонах Френеля (см. рисунок 6) амплитуда ре­зультирующего поля определяется алгебраическим суммированием, при этом учет фазы приводит к знакопеременному ряду. Каждый член ряда равен амплитуде поля, созданного в точке приема источниками п-й зоны:

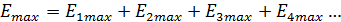
Для выявления количественных отношений удобно записать ряд в виде

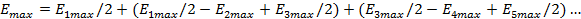
Поскольку соседние члены ряда мало отличаются друг от друга, то значение поля в каждой из скобок последнего выражения близко к нулю и в первом приближении результирующее поле

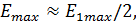
т.е. напряженность поля равна половине той величины, которая создается источниками первой зоны Френеля.

Результат последовательности от зоны к зоне алгебраического суммирования полей можно проследить по кривой, приведенной на рисунке 7. При суммировании полей от источников только первой зоны напряженность поля возрастает до Е = 2Е₀, где Е₀– поле в свободном пространстве.

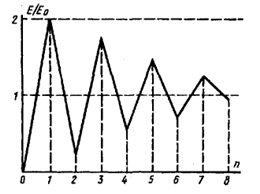
Рисунок 7. Результат алгебраического суммирования полей

При дальнейшем сложении проявляется действие про­тивофазных полей от источников второй зоны, и результирующая на­пряженность поля уменьшается. Компенсирующее действие полей от источников четных зон Френеля обусловливает немонотонный закон приближения величины Е к Е₀при → ∞.

Существенную область обычно ограничивают примерно восе­мью зонами Френеля. При таком приближении ошибка в вычислении поля не превышает 16 процентов. Выясним вопрос о пространственной форме существенной об­ласти. Соотношение (13) должно выполняться при любом положе­ИИ плоскости S₀ вдоль линии АВ (рисунок 8). Поэтому (13) является уравнением эллипсоида вращения. Таким образом, существенная область как пространственная фигура является эллипсоидом вращения с фокусами в точках передачи и приема.

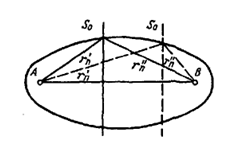
Рисунок 8. Пространственная форма существенной области

Внешний радиус n-й зоны Френеля ρ_n согласно рисунка 5, а и условию (13), а также с учетом того, что на реальных ли­ниях 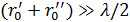, определяется соотно­шением

ρ_п = .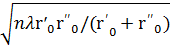

Максимальный радиус соответствует середине трассы, где 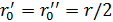и определяется

ρ_пmax = 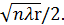(14)

Максимальный радиус существенного эллипсоида, ограничен­ного восемью зонами Френеля определяется

ρ_8max = = .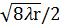

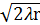Чем короче волна, тем меньше поперечные размеры существен­ного эллипсоида. Например, на волнах λ =10м…10см при протяжен­ности линии 10 километров радиус ρ_8max = 160…16 метров. При этом большая ось существенного эллипсоида, соизмеримая с длиной радиолинии, в сотни и тысячи раз больше его малой оси, т.е. эллипс сильно вытянут вдоль трассы.