Изучение явления дифракции света

Дифракцией света называется совокупность явлений, связанных с огибанием световыми волнами препятствий, их проникновением в область геометрической тени и образованием максимумов и минимумов интенсивности.

Дифракция световых волн может быть объяснена с помощью принципа Гюйгенса – Френеля, согласно которому:

- каждая точка волнового фронта является источником вторичных сферических волн, огибающая которых определяет форму волновой поверхности в следующий момент времени;

- все вторичные источники когерентны, поэтому в любой точке пространства параметры волны могут быть рассчитаны как результат интерференции всех вторичных волн;

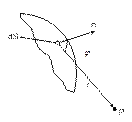- амплитуда вторичной сферической волны пропорциональна величине элемента волновой поверхности, убывает пропорционально расстоянию от источника и зависит от угла между нормалью к волновой поверхности и направлением распространения света (рис.1).

Рис. 1 Рис. 2

Расчет интерференции вторичных волн упрощается, если воспользоваться методом зон Френеля. Волновой фронт разбивается на зоны таким образом, чтобы расстояния от границ двух соседних зон до точки наблюдения отличались на λ/2 (рис.2). В этом случае разность хода лучей, идущих от любых двух соответствующих точек соседних зон в точке наблюдения, равна λ/2, и они придут в эту точку в противофазе, т.е. ослабят друг друга.

Различают два вида дифракции:

1) дифракция сферических волн (Френеля);

2) дифракция плоских волн или параллельных лучей (Фраунгофера).

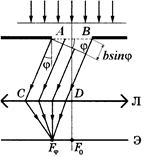Рассмотрим дифракцию монохроматических параллельных лучей с длиной волны λ на узкой щели шириной b. (рис.3). Согласно принципу Гюйгенса, каждая точка щели становится источником вторичных волн, которые распространяются за щелью во всех направлениях. Линза Л собирает дифрагированные параллельные лучи в соответствующих точках экрана Э, расположенного в ее фокальной плоскости, но при этом не вносит дополнительной разности хода волн.

Рис. 3 Рис. 4

Найдем условие максимума и минимума дифракции с помощью метода зон Френеля. Разобьем щель АВ на зоны, имеющие вид полос, параллельных ребру щели, так, чтобы расстояние от двух соседских полос до точки наблюдения М различалось на λ/2. Результат интерференции определяется тем, сколько зон укладывается на ширине щели. При четном числе зон в точке наблюдения будет минимум дифракции, при нечетном – максимум.

Поэтому условия дифракционного минимума и максимума, соответственно будут иметь вид:

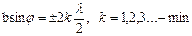(1)

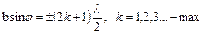(2)

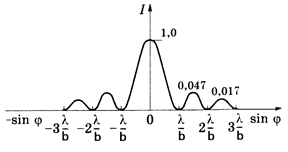
График распределения интенсивности света на экране представлен на рис. 4

Дифракционная картина усиливается, если перейти от одной щели ко многим. Это осуществляется в дифракционных решетках, состоящих из очень большого числа параллельных одинаковых и очень узких щелей, разделенных непрозрачными промежутками одинаковой ширины. Сумма ширины щели b и прозрачного промежутка a называется периодом дифракционной решетки:

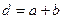(3)

При прохождении плоской волны света через решетку и дифракции от каждой щели прибавляется еще многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

В одном и том же направлении все щели излучают свет одинаково. Колебания от сходственных точек соседних щелей в точке М будут усиливать друг друга, если на их разности хода 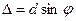будет укладываться четное число полуволн или целое число волн. Таким образом условие

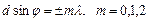… (4)

определяет положение главныхмаксимумов дифракционной решетки. Число m дает порядок главного максимума.

Для направлений, удовлетворяющих условию минимума от одной щели, будут наблюдаться минимумы и при многих щелях, поскольку ни одна из них не посылает света в этих направлениях. Таким образом, условие

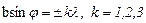… (5)

является также условием главныхминимумов решетки. Если дифракционная решетка состоит из N щелей, то кроме главных минимумов, определяемых условием (5), в промежутках между соседними главными максимумами имеется по (N-1) дополнительному максимуму. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Образование добавочных минимумов определяется условием

(6)

где P принимает все целочисленные значения, кроме 0,N,2N…, т.е. тех, при которых условие (6) переходит в (4).

Между дополнительными минимумами располагаются слабые вторичные максимумы. Число таких максимумов, находящихся в промежутке между соседними, главными максимумами равно (N-2).

При пропускании через решетку белого света все максимумы, кроме центрального разложатся в спектр, фиолетовый конец которого расположен к центру дифракционной картины, красный – наружу.

Дифракционные решетки являются главной частью дифракционных спектрометров – приборов, предназначенных для измерения длин волн электромагнитного излучения. Основными характеристиками спектрального прибора являются его дисперсия и разрешающая сила.

Дисперсия определяет угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу.

Угловая дисперсия

(7)

где dφ – угловое расстояние между спектральными линиями, отличающимися по длине волны на dλ.

Продифференцировав условие (4), получим

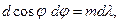
откуда

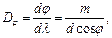(8)

В пределах малых углов

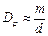(9)

Линейная дисперсия

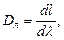(10)

где dl – линейное расстояние между спектральными линиями на экране, отличающимися по длине на dλ.

Линейная дисперсия может быть выражена через угловую дисперсию

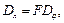
где F – допустимое расстояние линзы, собирающей дифрагирующие лучи на экране (рис. 5). При малых углах

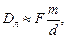(11)

Разрешающая способность дифракционной решетки определяется величиной

(12)

Рис. 5

где δλ – минимальная разность длин волн двух спектральных линий, при которой они воспринимаются раздельно. Два близких максимума воспринимаются глазом раздельно в том случае, если интенсивность в промежутке между ними составляет не более 80% от интенсивности максимума. Согласно критерию Релея такое соотношение имеет место в том случае, если середина одного максимума совпадает с ближайшим минимумом другого. Положения середины m – го главного максимума для длины волны λ+δλ определяются условием

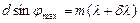(13)

Края m-го максимума для длины волны λ, удовлетворяют соотношению

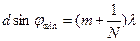(14)

Решая систему этих уравнений относительно λ/δλ, получаем

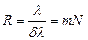(15)

Таким образом, разрешающая способность дифракционной решетки пропорциональна порядку спектра и числу щелей.

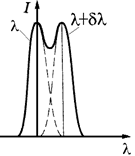
Рис. 6 Рис. 7

Методические указания к выполнению работы:

Задание 1. Наблюдение дифракционного спектра в белом свете.

Для выполнения данного упражнения используется оптическая скамья на которой установлены источники белого света, подвижный экран со щелью и дифракционная решетка. Дифракционный спектр рассматривается непосредственно на экране (рис. 8).

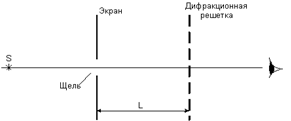
Рис. 8

Порядок выполнения

1. Включить источник света.

2. Установить экран от дифракционной решетки на расстоянии

15-20 см, чтобы на нем получалось четкое изображение центральной полосы и спектров первого и второго порядков.

3. Измерить ширину спектров первого и второго порядков.

4. Зарисовать полученные дифракционные спектры, обращая внимание на порядок следования цветов.

5. Сделать выводы.