Изучение явления интерференции

Интерференция света – явление наложения когерентных световых волн, в результате которого происходит перераспределение светового потока в пространстве (возникновение максимумов и минимумов интенсивности света). Когерентные волны – волны одинаковой частоты, разность фаз которых остается постоянной во времени, а плоскости колебаний световых векторов совпадают.

Естественные источники света не являются когерентными, поскольку излучение светящегося тела слагается из волн, испускаемых многими атомами. Отдельные атомы излучают цуги волн длительностью порядка 10^-8с и протяженностью около трех метров. Эти цуги, налагаясь друг на друга, образуют световую волну. Фаза световой волны изменяется с течением времени, поскольку излучение одной группы атомов сменяется излучением другой. Время, за которое случайные изменения фазы в световой волне достигают значения π, называют временем когерентности. За это время волна становится некогерентной к самой себе.

Для осуществления когерентности необходимо разделить один и тот же световой пучок на два и заставить их встретиться снова так, чтобы оптическая разность хода между интерферирующими лучами была меньше длины когерентности.

В зависимости от способа разбиения пучка на два существует два разных метода получения когерентных «источников»: метод деления волнового фронта и метод деления амплитуды. В методе деления волнового фронта, который пригоден только для достаточно малых источников, исходящий от источника пучок делится на два: либо проходя через два близко расположенных отверстия, либо отражаясь от зеркальных или полупрозрачных поверхностей (метод Юнга, бизеркала Френеля, бипризма Френеля, билинза Бийе, зеркало Ллойда и др.). Во втором методе, который пригоден как для малого, так и протяженного источников, световой пучок делится путем прохождения и отражения от полупрозрачной поверхности (интерференция от плоскопараллельной пластинки – полосы равного наклона, интерференция от пластинки переменной толщины – полосы равной толщины).

Оптическим путем называется произведение показателя преломления среды n на геометрическую длину пути S в данной среде:

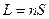(1)

Разность оптических длин, проходимых световыми волнами, называется оптической разностью хода:

(2)

Разность фаз налагаемых световых волн связана с их оптической разностью хода соотношением

(3)

где λ₀ – длина волны в вакууме.

Из этого соотношения следует, что если оптическая разность хода равна четному числу полуволн или целому числу длин волн в вакууме

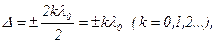(4)

то разность фаз δ оказывается кратной 2π, лучи в точку наблюдения приходят в одной фазе и амплитуда суммарной волны увеличивается, следовательно, соотношение (4) определяет условие интерференционного максимума.

Если ∆ равна нечетному числу полуволн в вакууме,

(5)

то 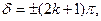так что колебания в точку наблюдения приходят в противофазе и гасят друг друга. Следовательно, условие (5) есть условие интерференционного минимума.

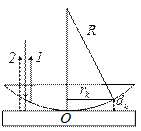
Интерференционную картину полос равной толщины можно наблюдать от воздушной прослойки, образованной плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой (рис. 1).

Рис.1.

При нормальном падении света, геометрическим местом точек одинаковой толщины является окружность, и поэтому соответствующие полосы равной толщины будут иметь вид концентрических окружностей с центром в точке

соприкосновения линзы с плоскопараллельной пластинкой. Отраженные от линзы и плоскопараллельной пластины лучи 1 и 2 распространяются практически вдоль одного направления. Их оптическая разность хода

(6)

где d – толщина воздушной прослойки, слагаемое λ∕2 учитывает изменение фазы волны на противоположную (потеря полуволны) при отражении от оптически более плотной среды (от плоскопараллельной пластинки).

Условия максимумов и минимумов интерференции для колец Ньютона имеют вид:

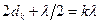(максимум); (7)

(минимум), (8)

где k=0,1,2,3…- порядок интерференционного максимума и минимума (очевидно, максимума 0-го порядка не будет);

d_k – толщины воздушного зазора, для которых будут наблюдаться светлые и темные интерференционные кольца.

Связь толщины воздушного слоя d_k с радиусом кривизны линзы R определяется из (рис. 1).

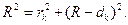
Так как R намного больше d_k, то величиной d_k² можно пренебречь, тогда

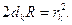(9)

Из формул (6) и (7) следует

(10)

Так как невозможно добиться идеального соприкосновения линзы с пластиной в одной точке, целесообразно вычислять длину волны по разности радиусов двух темных колец

, (11)

где k и m –номера интерференционных колец.