Крышка корпуса

Напряжение в стенке крышки оцениваем, рассматривая ее как кольцевую пластину, внешний край которой заделан по контуру радиуса R₁ и неподвижен, а внутренний край заделан и может прогибаться. Считаем, что пластина нагружена по всей поверхности равномерно распределенным давлением Р_у = 4 МПа. Принятая расчетная схема приведена на рисунке 2.3.

Максимальное напряжение определяется по формуле:

,

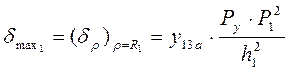где y_13a – коэффициент, зависящий от отношения r₁/R₁ ;

h₁ – толщина пластины, h₁ = 0,025 м.

при 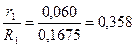; коэффициент y_13a = 0,53.

Тогда 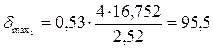МПа.

При этом на контуре радиуса R₁ ,будет действовать изгибающий момент интенсивностью:

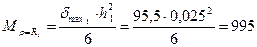Н•м/м.

Для оценки напряжения во фланце крышки рассмотрим его как

кольцевую пластину с защемленным внешним и свободным внутренним краем, находящуюся под действием:

1) контурной нагрузкой, суммарно равной Q, возникающей от действия гидростатического давления Р_у = 4 МПа на стенку крышки.

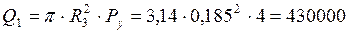Н

2) контурной нагрузкой, суммарно равной Q₂ , возникающей при сжатии двух спирально – навитых прокладок. (Условно удваиваем нагрузку от сжатия прокладки большего диаметра):

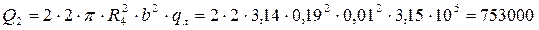Н.

Q₂ = 753000 H,

где b = 0,01 м – ширина прокладки;

q = 31,5 МПа – удельное давление необходимое для сжатия прокладки;

R₄ = 0,19 м – по рисунку 2.2;

3) изгибающего момента интенсивностью

М_ρ=R1 = 995 Н м/м.

Будем считать, что пластина защемлена по контуру расположения шпилек R₂ = 0,22 м.

За внутренний край пластины принимаем контур радиуса R₁ = 0,167 м.

Для упрощения расчета считаем, что контурная нагрузка Q₂ так же как и нагрузка Q₁ и момент М_ρ=R1 приложены по контуру R₁. Принятая расчетная схема показана на рисунке 2.3.

Напряжение на внешнем крае пластины :

,

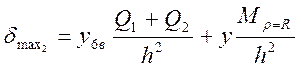при 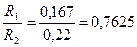коэффициент y_{6 в} = 0,13 и у =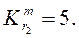

(коэффициент 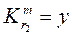получен линейкой интерполяцией). Подставив значение в приведенную выше формулу, получим:

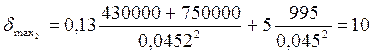МПа.