Ємності переходу

Залежно від фізичної природи заряду, що змінюється в переході, розрізняють бар’єрну та дифузійну ємності.

Бар’єрна (зарядова) ємність визначається зміною нескомпенсованого заряду іонів при зміні товщини запірного шару під дією зовнішньої напруги. Ідеальний 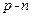- перехід нагадує плоский конденсатор, пластинами якого є нейтральні низькоомні області НП. Отже, при використанні формули (1.32) бар’єрна ємність дорівнює

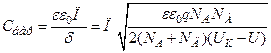. (1.36)

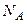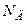З (1.36) випливає, що бар’єрна ємність збільшується при зростанні і , а також при зростанні прямої напруги. При зростанні зворотної напруги бар’єрна ємність зменшується. Характер залежності 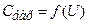показано на рисунку 1.15.

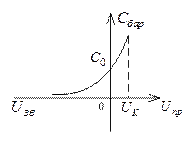
Рисунок 1.15 – Вольт-фарадна характеристика р-n-переходу

Дифузійна ємність зумовлена здебільшого процесами інжекції. Зміну заряду неосновних носіїв відносно рівноважного рівня біля переходу при зміні прямої напруги можна розглядати як прояв деякої ємності:

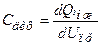, (1.37)

де 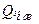- величина інжектованого заряду.

Величина цієї ємності може бути розрахована за формулою

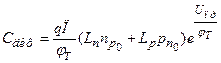. (1.38)

Як правило, при прямому ввімкненні 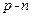- переходу враховується лише дифузійна ємність, тому що бар’єрна ємність становить одиниці пікофарад, а дифузійна – десятки нанофарад.

Ємності переходу враховуються при складанні його еквівалентної схеми (рис. 1.16). На схемі 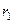- розподілений опір р- та n-областей; 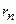- поверхневий опір (для струмів поверхневого витоку); 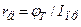- диференціальний опір переходу.

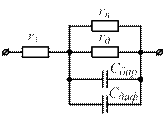
Рисунок 1.16 – Еквівалентна схема р-n - переходу

Для кімнатної температури ( 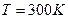) справедлива формула Шоклі

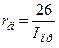, (1.39)

де 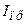подають у міліамперах.

При прямому вмиканні 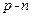- переходу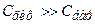 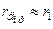, тому еквівалентна схема набирає вигляду рис. 1.17 а. При зворотному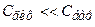 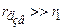, і спрощена еквівалентна схема переходу має вигляд рис. 1.17 б.

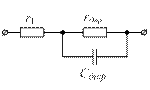
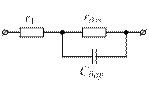
а) б)

Рисунок 1.17 – Еквівалентна схема р-n - переходу:

а) при прямому вмиканні; б) при зворотному вмиканні