Бинарная и мультиномиальная логистические регрессии
В настоящем разделе мы рассмотрим два основных типа логистической регрессии — бинарную и мультиномиальную, а также дадим общий обзор порядковой логистической регрессии. Цель статистического анализа при применении методов логистической регрессии — определить вероятность того, что тот или иной респондент (на основании определенных характеристик) попадет в ту или иную целевую группу. На практике описываемые методы, согласно значениям одной или нескольких независимых переменных (факторов), позволяют классифицировать респондентов по двум (бинарная) или более (мультиномиальная) группам, которые выражаются уровнями (вариантами ответа) какой-либо одной переменной.
Например, имеются ответы респондентов на вопрос Интересно ли Вам предложение о покупке земельного участка недалеко от Москвы? с вариантами ответа Да и Нет. Требуется выяснить, какие факторы в наибольшей степени определяют решение потенциальных покупателей о приобретении земельного участка. Для этого респондентам задается ряд вопросов с просьбой указать, какие элементы инфраструктуры им необходимы на данном участке, какое расстояние от Москвы является для них оптимальным, каков должен быть размер данного участка, должен ли на участке быть дом и т. п. Используя в данном случае метод бинарной логистической регрессии, можно классифицировать всех респондентов по двум целевым группам: заинтересованные в покупке земельного участка (потенциальные покупатели) и не заинтересованные. Также для каждого респондента в выборке будет рассчитана вероятность попадания в ту или иную группу.
Различие между рассматриваемыми двумя методами логистической регрессии заключаются в количестве категорий и типе зависимой переменной, а также типе независимых переменных. Так, в случае бинарной логистической регрессии исследуется зависимость дихотомической переменной от одной или нескольких независимых переменных, имеющих любой тип шкалы. Мультиномиальная логистическая регрессия является разновидностью бинарной, в которой зависимая переменная имеет более двух категорий. Независимые переменные должны относиться либо к номинальной, либо к порядковой шкале.
Еще в версии SPSS 11-12 был введен новый метод логистической регрессии: порядковая. Он используется в том случае, когда зависимая переменная относится к порядковой шкале. Причем независимые переменные должны быть либо номинальными, либо порядковыми. Мультиномиальный логистический регрессионный анализ является наиболее универсальным и, в целом, способен заменить собой два других метода. Однако наиболее качественное приближение статистических моделей может быть достигнуто только при использовании именно трех описываемых методов: для каждого случая — свой. В табл. 5.1 систематизированы основные характеристики переменных, участвующих в рассматриваемых трех типах логистического регрессионного анализа.
Таблица 5.1. Основные характеристики переменных, участвующих в анализе
| Бинарная логистическая регрессия | ||||
| Зависимые переменные | Независимые переменные | |||
| Количество | Тип | Количество | Тип | |
| Она | Дихотомическая | Любое | Любой | |
| Мультиноминальная логическая регрессия | ||||
| Зависимые переменные | Независимые переменные | |||
| Количество | Тип | Количество | Тип | |
| Одна | Номинальная Порядковая | Любое | Номинальная Порядковая | |
| Порядковая логистическая регрессия | ||||
| Зависимые переменные | Независимые переменные | |||
| Количество | Тип | Количество | Тип | |
| Одна | Порядковая | Любое | Номинальная Порядковая | |
Необходимо отметить, что ранее в SPSS отсутствовала стандартная возможность проведения специализированного логистического регрессионного анализа для зависимых переменных с порядковой шкалой. Для любых переменных с числом категорий больше двух применялся мультиномиальный регрессионный анализ. Дело в том, что недавно введенная в практику анализа порядковая логистическая регрессия имеет некоторые особенности, учитывающие именно специфику порядковой шкалы (связанных упорядоченных категорий). Однако в настоящем пособии порядковая логистическая регрессия не рассматривается отдельно — в первую, очередь из-за того, что она не обладает какими-либо существенными преимуществами над мультиномиальным методом. Вы можете спокойно применять мультиномиальную регрессию и в случае номинальной, и в случае порядковой зависимой переменной. Если вы все же решите провести порядковый логистический регрессионный анализ, вы без труда в нем разберетесь, так как данный процесс практически не отличается от построения мультиномиальной логистической регрессии.
Далее мы рассмотрим примеры проведения статистического анализа с использованием логистической регрессии отдельно для бинарной и мультиномиальной логистической регрессии.
Начнем с наиболее простого случая — бинарной логистической регрессии. Предположим, в ходе маркетингового исследования проводится оценка востребованности выпускников одного из московских вузов. В анкете респондентам в числе прочих задаются три вопроса:
■ Работаете ли вы? (ql);
■ В каком году Вы окончили вуз? (q21);
■ Каков был Ваш средний балл при выпуске из вуза? (aver), а также уточняется пол опрошенных (q22).
В ходе логистического анализа мы оценим влияние независимых переменных q21, q22 и aver на зависимую переменную ql. Другими словами, мы попытаемся предсказать трудоустройство выпускников вуза на основании пола, года окончания вуза и среднего балла, полученного за годы обучения.
Для того чтобы задать параметры построения регрессионной модели при помощи бинарного логистического метода, воспользуемся меню Analyze ► Regression ► Binary Logistic. В открывшемся диалоговом окне Logistic Regression (рис. 5.1) выберите в левом списке всех доступных переменных зависимую (в нашем случае ql) и поместите ее в поле Dependent. Затем в область Covariates поместите исследуемые независимые переменные (q21, q22, aver) и выберите метод их включения в регрессионный анализ. При числе независимых переменных больше двух следует выбрать не установленный по умолчанию метод одновременного включения всех переменных (Enter), а один из пошаговых. Наиболее часто используемым пошаговым методом является Backward:LR. Кнопка Select позволяет включить в анализ не всех респондентов из выборочной совокупности, а только отдельную целевую группу.
 |
|
 |
Кнопкой Categorical следует воспользоваться, если в качестве одной из независимых переменных выступает номинальная переменная с числом категорий больше двух. В данном случае в диалоговом окне Define Categorical Variables (рис. 5.2) следует поместить в область Categorical Covariates такую переменную (в нашем случае таких переменных нет). Далее следует выбрать в раскрывающемся списке Contrast пункт Deviation и щелкнуть на кнопке Change. В результате из каждой номинальной переменной будет создано несколько дихотомических переменных (по числу категорий исходной переменной).
|
При помощи кнопки Save в главном диалоговом окне анализа (рис. 5.3) можно задать создание новых переменных, содержащих значения, рассчитанные в ходе регрессионного анализа. Так давайте создадим две новые переменные, содержащие:
■ принадлежность к определенной группе классификации (параметр Group membership);
■ вероятность попадания респондента в каждую из двух рассматриваемых групп (параметр Probabilities).
|
 |
Кнопка Options не предоставляет исследователю никаких важных возможностей, поэтому ее можно не использовать. После щелчка на кнопке О К в главном диалоговом окне Logistic Regression в окне SPSS Viewer будут выведены результаты бинарного логистического регрессионного анализа.
Далее мы рассмотрим наиболее существенные для маркетингового анализа результаты. В таблице Omnibus Tests of Model Coefficients отображаются результаты оценки
качества приближения статистической модели (рис. 5.4). Поскольку мы задали пошаговый метод, мы должны смотреть на результаты последнего шага (в нашем случае Step 2). Положительным результатом считается возрастание величины Chi-square при переходе на каждый следующий шаг (строка Step) при высоком уровне значимости (Sig. < 0,05). Качество всей модели оценивается на основании статистической значимости в строке Model. В нашем случае на втором шаге получена отрицательная величина Chi-square, однако она не является значимой (Sig. = 0,913), к тому же общая значимость всей модели весьма высока (Sig. < 0,001). Поэтому построенную модель следует признать значимой и практически пригодной.
|
 |
Следующая таблица Model Summary (рис. 5.5) позволяет оценить долю совокупной дисперсии, описываемой построенной моделью (величина R Square). Рекомендуется использовать величину Nagelkerke. В нашем случае эта величина мала (лишь 6 %). Положительным результатом можно считать величину Nagelkerke R Square, превышающую 0,50.
 |
|
Далее следуют результаты классификации (таблица Classification Table, рис. 5.6), в которой реально наблюдаемые показатели принадлежности к той или иной из двух исследуемых групп сопоставляются с предсказанными на основе логистической регрессионной модели. В нашем случае из строки Overall Percentage мы видим, что построенная модель позволяет корректно классифицировать 80,4 % респондентов. Также можно сделать соответствующие выводы о корректности классификации для каждой из двух рассматриваемых групп.
Из следующей таблицы (рис. 5.7) можно выяснить статистическую значимость независимых переменных, включенных в анализ (в нашем случае q22 и aver), а также нестандартизированные регрессионные коэффициенты, являющиеся коэффициентами регрессионной функции. На основании этих коэффициентов (включая константу Constant) вы можете спрогнозировать принадлежность к определенной группе каждого конкретного респондента в выборке. Это делается следующим образом.
 |


Например, выпускник вуза получил средний балл 3,3 (aver = 3,3); это женщина (q22 = 2). В таком случае уравнение регрессии будет выглядеть следующим образом:
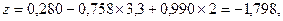
а вероятность для рассматриваемого респондента оказаться в одной из анализируемых групп классификации (это всегда группа зависимой переменной, имеющая больший код, в нашем случае 2 — Не работают) будет рассчитываться по формуле:
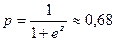
Таким образом, женщина со средним баллом 3,3 имеет достаточно высокие шансы оказаться безработной (68 %).
Теперь рассмотрим пример проведения мультиномиальной логистической регрессии. В качестве исходных данных мы будем использовать три независимые переменные из предыдущего примера, а в качестве зависимой — переменную q24 Заработная плата с пятью категориями, кодирующими интервалы зарплаты.
Откройте диалоговое окно Multinomial Logistic Regression при помощи меню Analyze ► Regression ► Multinomial Logistic (рис. 5.8). В поле для зависимой переменной поместите переменную q24, а в область для зависимых переменных — q21, q22 и aver.
Кнопка Model позволяет задать конкретный тип модели (полнофакторная, основные эффекты или пользовательская), однако для маркетинговых исследований мы советуем ничего не менять в окне Model.
При помощи кнопки Statistics вызывается одноименное диалоговое окно (рис. 5.9). В нем следует оставить выбранные по умолчанию три параметра: Summary statistics, Likelihood ratio test и Parameter estimates, а также выбрать еще один пункт — Cell Probabilities.
 |
|
 |
|
Кнопка Criteria не предоставляет маркетологам существенных для решения их задач функций, поэтому используется редко.
При помощи кнопки Save (рис. 5.10) можно задать новые переменные, содержащие принадлежность к определенной классификационной группе (параметр Predicted category) и вероятность попадания в данные категории (параметр Predicted probabilities membership).
После щелчка на кнопке 0К в главном диалоговом окне Multinomial Logistic Regression в окне SPSS Viewer появятся результаты расчетов. Первая таблица, содержащая важные для нас сведения, — это Model Fitting Information, показанная на рис. 5.11. Высокая статистическая значимость построенной модели (Sig. < 0,001) свидетельствует о ее высоком качестве и пригодности для решения практических задач.
Вторая значимая таблица Pseudo R-Square предоставляет возможность оценить долю совокупной дисперсии в зависимой переменной, объясняемой выбранными для анализа независимыми переменными (по тесту Nagelkerke). В нашем случае построенная модель объясняет 15 % совокупной дисперсии (рис. 5.12).
Таблица Likelihood Ratio Tests (рис. 5.13) позволяет сделать выводы относительно статистической значимости каждой из зависимых переменных, входящих в построенную модель. В нашем случае все три исследуемые переменные оказывают весьма значимое влияние на зависимую переменную (Sig. < 0,05).
 |
|
 |
|
 |
|
 |
|
 |
|
Следующая таблица, Parameter Estimates (рис. 5.14), отражает нестандартизированные регрессионные коэффициенты, на основании которых происходит построение регрессионного уравнения. Также для каждого сочетания анализируемых переменных рассчитана статистическая значимость их влияния на зависимую переменную. В дальнейшем рассчитать вероятность попадания того или иного респондента в одну из исследуемых групп зависимой переменной можно по вышеприведенной формуле (показана при обсуждении бинарной логистической регрессии).
Однако в маркетинговых исследованиях чаще всего возникает необходимость классифицировать по группам не отдельных респондентов, а целые целевые группы. Для этого служит таблица Observed and Predicted Frequencies, представленная на рис. 5.15. В столбце Percentage ► Predicted показаны вероятности попадания каждой исследуемой целевой группы респондентов в ту или иную категорию зависимой переменной. Так, например, мы видим, что 20 % мужчин, окончивших ВУЗ в 2001 г. и получивших средний балл 3,0, зарабатывают до $ 400 в месяц.

|
Дата добавления: 2015-04-25; просмотров: 1392;
