Дифракция света. Принцип Гюйгенса-Френеля.

Принцип Гюйгенса-Френеля.

В предыдущих лекциях мы уже знакомились с понятием дифракции и дифракционными явлениями, связанными с непрямолинейным распро-странением волн, огибанием ими препятствий и проникновением их в область геометрической тени.

Дифракция звуковых волн наблюдается в обыденной жизни. Для наблюдения дифракции световых волн необходимо создание специальных условий. Это обусловлено тем, что масштабы дифракции сильно зависят от соотношения размеров препятствия и длины волны.

Световые волны имеют малую длину волны, поэтому для наблюдения дифракции размеры препятствия должны быть ничтожно малыми. Или иначе говорят, что для световых волн дифракция выражена слабо.

Мы уже объясняли явление дифракции с помощью принципа Гюйгенса. Однако он не дает никаких указаний об амплитуде и, следовательно, интенсивности волн, распространяющихся в различных направлениях. Этот недостаток был устранен Френелем, который дополнил принцип Гюйгенса представлением об интерференции вторичных волн.

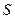Пусть представляет собой волновую поверхность света, распространяющегося от некоторого источника. Каждый элемент поверхности, согласно Френелю, служит источником вторичных сферических волн. Амплитуда этих волн пропорциональна величине элемента 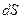. От каждого элемента 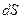в некоторую точку пространства 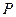приходит колебание

,

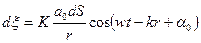где 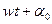- фаза колебаний;

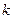- волновое число;

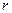- расстояние от элемента поверхности 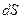до точки ;

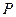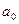- амплитуда светового давления.

Результирующее колебание в точке 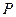представляет собой суперпозицию таких колебаний, взятых для всей волновой поверхности .

,

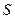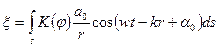где 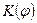- есть некоторая функции угла 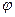между направлением внешней нормали к элементу волновой поверхности и направлением радиус-вектора 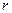. Согласно гипотезе Френеля, 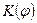имеет максимальное значение при и далее медленно убывает с ростом 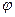, превращаясь в нуль при .

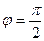Последнее выражение можно рассматривать как аналитическое выражение принципа Гюйгенса-Френеля. Вычисления по этой формуле представляют собой чрезвычайно трудную задачу. Для упрощения расчетов Френелем был предложен метод разделения фронта волны на зоны, рас-положенные таким обра-зом, что колебания, приходящие в рассма-триваемую точку про-странства от двух со-седних зон, находятся в противофазе. Тогда на-хождение амплитуды ре-зультирующего колебания сводится к простому геометрическому cум-мированию.

Прежде чем перейти к детальному рассмотрению этого метода отметим, что существуют два вида дифракции:

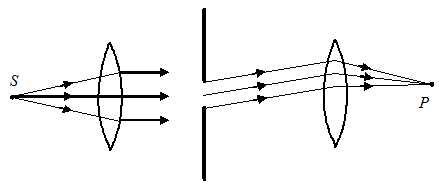
1. Если источник света и точка наблюдения расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку наблюдения, образуют параллельные пучки, то такой вид дифракции называется дифракцией Фраунгофера. Для практического осуществления этого типа дифракции источник света помещают в фокусе собирающей линзы, а дифракционную картину наблюдают в фокальной плоскости второй собирающей линзы, установленной позади препятствия.

2. Если источник света и точка наблюдения находятся в непосредственной близости от препятствия, то лучи, падающие на препятствие, и лучи, идущие в точку наблюдения, не являются параллельными. Такой вид дифракции называется дифракцией Френеля.

Расчет дифракционных явлений наиболее удобно, как мы уже заметили, производить с помощью метода зон Френеля. Рассмотрим этот метод подробнее.

Зоны Френеля

Применим принцип Гюйгенса-Френеля для нахождения амплитуды светового колебания, возбуждаемого в точке « » сферической волной, распространяющейся в однородной среде из точечного источника .

Волновая поверхность такой волны симметрична относительно прямой . Разобьем волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки отличаются на .

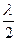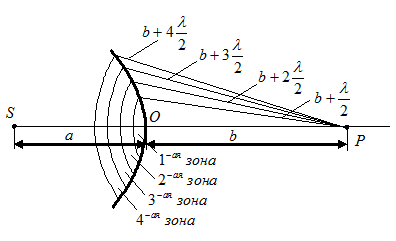В общем виде расстояние от внешнего края зоны до точки можно представить как

,

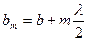где 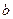- расстояние от вершины волновой поверхности 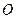до точки ;

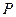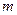- номер зоны;

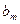- расстояние от точки 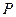до внешнего края зоны.

Колебания, приходящие в точку 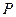от двух соседних зон, будут находиться в противофазе.

Для оценки амплитуд колебаний нужно найти площади зон. Обозначим через 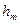расстояние от точки 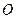до точки пересечения внешней границы зоны с прямой 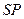, и через 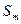- площадь участка волновой поверхности, заключенного между внешней границей зоны и точкой .

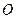Тогда площадь любой зоны 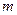будет равна:

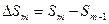, (1)

где 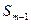- площадь всех предыдущих зон.

Площадь 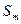, как следует из геометрических построений, равна

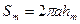. (2)

Выделим на волновой поверхности произвольную кольцевую зону и рассмотрим ее более подробно.

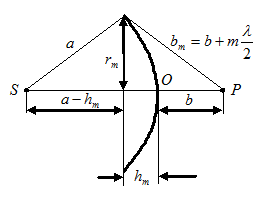Как следует из рисунка

.

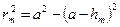С другой стороны

.

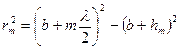Приравняв оба равенства, получим

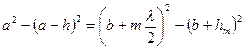
или, раскрыв скобки и произведя необходимые сокращения,

.

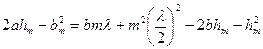Откуда

.

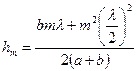Ограничившись рассмотрением небольших значений « 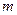», ввиду малости значения 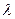, слагаемым, содержащим 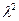, пренебрежем.

Тогда

.

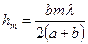Подставив это значение 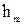в формулу (2) для 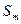, получим

.

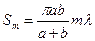Подставив это значение 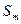в формулу (1) для 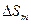, получим

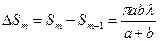- площадь любой зоны Френеля (не зависит от ).

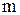Найдем формулу для радиусов зон Френеля.

Как видно из чертежа, 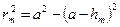или же, раскрыв скобки, .

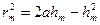Для небольших значений « 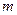» 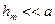и поэтому величиной 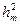можно пренебречь.

Тогда, .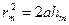

Подставив вместо 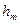ее выражение, получим радиус внешней границы любой зоны Френеля .

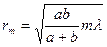Как мы уже заметили, расстояние 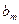от точки 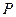до зоны « 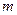» растет с ростом номера зоны. При этом также растет угол между нормалью к элементам зоны и направлением на точку 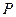(угол 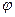). Все это приводит к тому, что амплитуда колебаний в точке 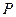от каждой зоны монотонно убывает с ростом « 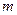», т.е.

.

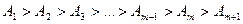Фазы колебаний, возбуждаемых соседними зонами, отличаются на 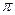. Поэтому амплитуда результирующих колебаний в точке 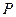равна

.

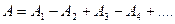Запишем это выражение несколько в ином виде

.

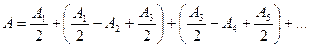Вследствие монотонного убывания амплитуды колебаний с ростом номера зоны можно считать, что амплитуда любой зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.

.

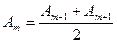Поэтому в предыдущем уравнении выражения, стоящие в скобках, равны нулю и формула примет вид

.

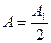Это значит, что амплитуда, создаваемая в некоторой точке 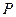сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной.

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, амплитуда в точке 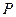будет равна 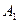, т.е. в два раза больше, чем при отсутствии преград между 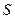и .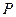

Переходя к интенсивности можно сказать, что интенсивность света, создаваемого центральной зоной Френеля, в 4 раза превышает интенсивность, создаваемую всей волновой поверхностью.

Колебания четных и нечетных зон Френеля находятся в противофазе и взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая бы перекрывала все четные или нечетные зоны, то амплитуда колебаний в точке 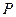резко возрастает. Такая пластинка называется зонной. Такая зонная пластинка, перекрывающая четные зоны, изображена на рисунке.

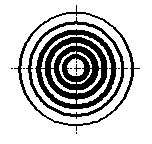Зонная пластинка во много раз увеличивает интенсивность света в точке 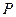, действуя подобно собирательной линзе.

Еще большего эффекта можно достигнуть, не перекрывая четные или нечетные зоны, а, изменяя их фазу на 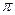. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на величину, выбранную определенным образом. Такая пластинка называется фазовой зонной пластинкой.

По сравнению с обычной зонной пластинкой, фазовая дает дополнительное увеличение амплитуды в 2 раза, а интенсивности света – в 4 раза.