МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТЕПЛОПЕРЕДАЧИ ЧЕРЕЗ ОГРАЖДАЮЩИЕ КОНСТРУКЦИИ
Здание представляет собой сложную архитектурно-конструктивную систему с многообразием составляющих ее элементов ограждающих конструкций и инженерного оборудования. Под действием разности температур наружного и внутреннего воздуха и солнечной радиации помещение через ограждающие конструкции в зимнее время теряет, а в летнее получает теплоту. Гравитационные силы, действие ветра и вентиляция создают перепады давлений, приводящие к перетеканию воздуха между сообщающимися помещениями и к его фильтрации через поры материалов и неплотности ограждений. Атмосферные осадки, влаговыделения в помещениях, разность влажности внутреннего и наружного воздуха приводят к влагообмену через ограждения, под влиянием которого возможно увлажнение материалов и ухудшение их теплозащиты.
Ограждающие конструкции играют определяющую роль в тепловом балансе здания. На рисунке 2.1 приведен пример теплового баланса здания старой постройки в сравнении с тепловым балансом энергоэффективного здания. В левой колонке показаны тепловые потери, а в правой - теплопоступления. Разница (не закрашенная область) показывает расход энергии на отопление Н, который можно снизить с 400 кВт•ч/м2, затрачиваемых в настоящее время в зданиях старой постройки, до 40 кВт•ч/м2(здания с ультранизким энергопотреблением), то есть расход энергии на отопление уменьшается в 10 раз. Такие балансы можно составлять без особых усилий. Каждая отдельная составляющая баланса (V, Т, S, I, R, H) просто должна быть графически сложена с остальными, как это показано на рисунке 2.1 .
Если в зданиях старой постройки применять современную высокоэффективную теплоизоляцию, не используя другие возможности снижения энергопотребления, то можно сэкономить существенное количество энергии. Таким образом, очень важным элементом является теплоизоляция наружных стен здания. Конструкция окон также оказывает существенное влияние на тепловую эффективность здания, как за счет теплопотерь, так и за счет инфильтрации. Отметим, что оптимизация формы, размеров и конструкции заполнений светопроемов позволяет обеспечить дополнительную экономию энергии за счет использования естественного освещения. Из этого можно сделать вывод, что для достижения удовлетворительного общего теплового баланса здания, конструкция окон должна быть гармоничной - не только в отношении внешнего вида фасада и конструкции, но и в отношении ориентации зданий в пространстве (беря во внимание расположение соседних конструкций, закрывающих внутреннее пространство).
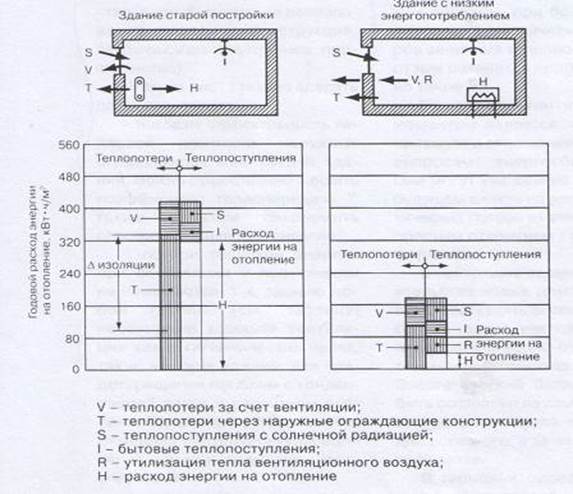
Рисунок 2.1- Годовой тепловой баланс здания старой постройки и здания с
ультранизким энергопотреблением
Итак, из рисунка 2.1 можно сделать следующие выводы:
- повысив эффективность тепловой изоляции наружных ограждающих конструкций здания, можно существенно снизить коэффициент теплопередачи Т, таким образом сэкономить огромное количество энергии;
- потери тепловой энергии при вентиляции V практически не изменяются, так как зданию любой группы необходима хорошая вентиляция как в гигиенических целях, так и, что еще важнее, для предотвращения проблем с конденсацией влаги и развитием плесени. Однако при установке современной системы рекуперации тепла можно использовать часть энергии R;
- количество дополнительной тепловой энергии, полученной за счет солнечной энергии S, в энергоэффективном здании останется приблизительно на том же уровне, что и в здании старой постройки;
- величина энергии бытовых теплопоступлений I останется приблизительно такой же, как и сейчас, так как количество бытовых электрических приборов в жилых помещениях в будущем возможно и увеличится, но и эффективность бытовой техники постоянно повышается. Таким образом, при большем количестве электрических приборов величина теплопоступления от них останется приблизительно такой же.
Еще раз отметим, что важным моментом является изменение привычек и отношения жильцов к вопросам энергосбережения. Они могут уже сейчас и смогут в будущем влиять на долю энергетических потерь от вентиляции V простым открытием или закрытием форточки.
В настоящее время при строительстве новых домов необходимо составлять энергетический баланс здания, учитывающий теплопотери и тепло от дополнительных источников энергии. Энергетический баланс должен быть составлен на самом раннем этапе строительства, еще на стадии эскизного, а затем и рабочего проекта.
В Европейских странах уже существуют жилые здания, способные обеспечивать свои собственные энергетические потребности. У этих зданий высокоэффективная теплоизоляция стен, окон и крыши.
Например, в одном из таких зданий потребность в электроэнергии покрывается за счет фотогальванических элементов, установленных на крыше. Более того, на крыше установлены солнечные коллекторы, способные нагревать, особенно в летнее время, хорошо изолированный водяной бак объемом около 10 м3. Этот водяной бак расположен в подвале, на месте «масляного бака», который уже не используется. Водяной бак является системой аккумуляции сезонной энергии, и позволяет использовать в зимнее время часть солнечной энергии, накопленной летом.
В проектах подобных домов следует учитывать расход энергии за весь период жизненного цикла здания, то есть расход энергии на строительство, эксплуатацию, снос и утилизацию здания. При расчете жизненного цикла здания необходимо учесть не только потоки энергии, но и потоки материалов и отходов. Иначе для здания с низким энергопотреблением, но построенного с большими энергетическими затратами, общие затраты энергии за период жизненного цикла могут оказаться очень велики.
Решающим значением для любой национальной экономики и экологического успеха в области сбережения энергии, затрачиваемой на отопление, является принятие адекватных энергосберегающих мер не только в отношении новых строящихся зданий, но и уже существующих зданий старой постройки. Повышение энергетической эффективности существующих зданий должно неукоснительно выполняться параллельно с модернизацией их конструктивных элементов. Очевидно, что создание в XXI веке городов с нулевыми выбросами возможно только в случае энергетической модернизации большого количества зданий старой постройки. Этого невозможно добиться за несколько лет, но такая задача должна быть поставлена и выполнена в течение оставшихся 90 лет этого столетия.
В настоящее время для построения и реализации математических моделей сложных энергетических объектов, к которым может быть отнесено здание, используется методология системного подхода [1] .
На рис. 2.2 показана упрощенная схема теплового баланса помещения.
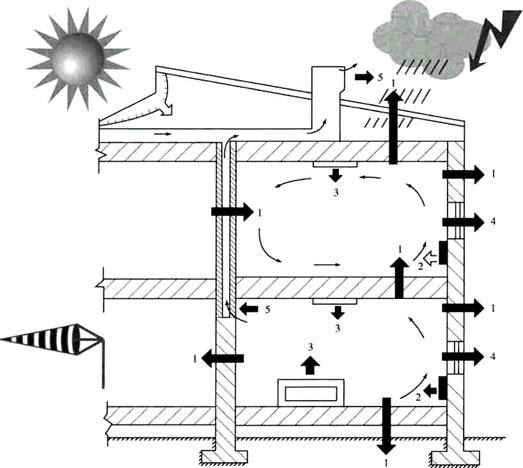
Рисунок 2.2- Схема теплового баланса здания:
1 - теплопотери или теплопоступления через ограждающие конструкции
(стены, покрытия, перекрытия и т.д.);
2 - тепловыделения от отопительных приборов;
3 - теплопоступления от технологического оборудования;
4 - теплопотери или теплопоступления через заполнение светового
проема;
5 - теплопотери за счет воздухообмена
В общем случае ограждающие конструкции являются неоднородными и могут содержать вентилируемые или замкнутые воздушные прослойки, а также источники тепла. При определении математической модели теплопередачи через ограждающую конструкцию авторы монографии [2] приняли следующие допущения:
- теплотехнические характеристики материалов слоев не зависят от влажности и температуры материала;
- влияние откосов оконного проема, стыков, наружных углов, теплопроводных включений на деформацию температурного поля ограждения корректируется с помощью введения эквивалентных теплотехнических показателей, так что температурное поле конструкции можно считать одномерным;
- теплопередача через конструкцию происходит за счет теплопроводности и фильтрации воздуха;
- имеют место потери (выделения) тепла, связанные с замерзанием (таянием) влаги в материале.
Следует отметить, что при развитии математического описания процессов теплопередачи через ограждающие конструкции необходимо учитывать изменение теплотехнических характеристик материалов при их увлажнении. Известно, что сопротивление теплопередаче ограждающих конструкций при увеличении влажности материалов на 1% может уменьшиться на 8-15%. Наряду с погодными условиями, температурой, солнечным излучением и влажностью воздуха на наружные стены часто воздействуют внешние и внутренние источники влаги, например, косые дожди, строительная влажность, образующийся конденсат.
Далее приведено математическое представление модели теплопередачи через ограждающие конструкции, выполненное Табунщиковым Ю.А. и Бродач М.М. [2]. С учетом принятых ими выше указанных допущений уравнение теплопроводности для конструкции имеет вид:
|
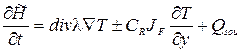
где
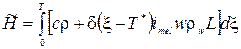
T*- температура фазового перехода вода-лед, °С;
L - льдистость материала, доли единицы;
w - весовая влажность материала, доли единицы;
ρw - плотность воды, кг/м3;
imel - удельная теплота фазового перехода, Дж/кг;
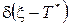 - дельта-функция Дирака;
- дельта-функция Дирака;
JF - расход воздуха через единицу поверхности ограждения, кг(м2·ч);
Qsou - удельная мощность источников тепла в ограждении, Вт/м3;
СR - удельная теплоемкость воздуха, Дж/(кг°С);
С, ρ - соответственно удельная теплоемкость в Дж/(кг°С) и плотность материалов слоев ограждения, кг/м3, при этом:
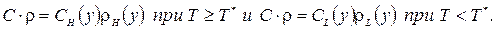
|
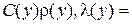
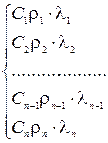
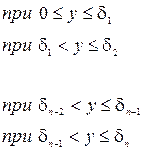
Сi, ρi, - произведение удельной теплоемкости материала слоя ограждения, Дж/(кг·°С), на его плотность, кг/м3, (i=1,2,3,…,п);
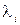 - коэффициент теплопроводности материала слоя ограждения, Дж/(кг·°С), (i=1,2,…,n);
- коэффициент теплопроводности материала слоя ограждения, Дж/(кг·°С), (i=1,2,…,n);
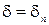 - толщина ограждения, м;
- толщина ограждения, м;
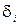 - расстояние от наружной поверхности ограждения до конца i-го слоя, м, (i=1,2,...,n).
- расстояние от наружной поверхности ограждения до конца i-го слоя, м, (i=1,2,...,n).
При выводе уравнения (2.1) был использован метод математического описания задач Стефана /7/, заключающийся в том, что граница раздела фаз (вода-лед) не выделяется в отдельное граничное условие, а «включается» в уравнение теплопроводности. Влияние выделения или поглощения тепла при фазовом переходе учитывается добавлением к «истинной» теплоемкости добавочного члена
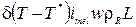
Для ограждений с источником тепла типа греющий кабель удельная мощность источника тепла может быть вычислена в предположении, что он является точечным, по формуле:
|
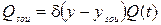
где
Q(t) - мощность источника, Вт/м2;
ysou - расстояние от наружной поверхности ограждения до плоскости расположения источника, м;
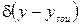 - дельта-функция Дирака, 1/м.
- дельта-функция Дирака, 1/м.
Для покрытий со слоем воды[1] удельная мощность источника тепла может быть вычислена по формуле:
|
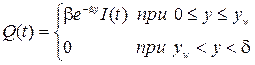
где
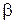 - показатель затухания интенсивности потока суммарной солнечной радиации при прохождении через слой воды, 1/м;
- показатель затухания интенсивности потока суммарной солнечной радиации при прохождении через слой воды, 1/м;
I(t) - интенсивность потока суммарной солнечной радиации, падающей на покрытие, Вт/м2;
yw - толщина слоя воды на покрытии, м.
Температурное поле многослойного ограждения, имеющего замкнутые воздушные прослойки, описывается также уравнением, эквивалентным (2.2). При этом с·ρ - объемная теплоемкость воздуха, а значение коэффициента теплопроводности определяется по формуле 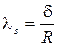 , где
, где 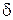 - толщина прослойки, м; R - термическое сопротивление воздушной прослойки с учетом конвективного и лучистого теплообмена, м2·°С/Вт.
- толщина прослойки, м; R - термическое сопротивление воздушной прослойки с учетом конвективного и лучистого теплообмена, м2·°С/Вт.
Определение расхода воздуха через единицу поверхности ограждения производится на основе следующих предположений: при расчете давления на наружной поверхности ограждения принимаем, что к рассматриваемому явлению применим принцип независимости действия сил гравитационного и ветрового давления; связь между давлением и температурой определяется уравнением состояния Клапейрона; уравнение проводимости воздуха элементом конструкции имеет вид 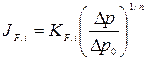 , где КF,i - коэффициент проводимости воздуха элементом конструкции, равный расходу воздуха через единицу площади конструкции при разности давлений
, где КF,i - коэффициент проводимости воздуха элементом конструкции, равный расходу воздуха через единицу площади конструкции при разности давлений 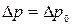 , кг/(м2·ч);
, кг/(м2·ч); 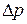 - разность давлений воздуха на наружной и внутренней поверхностях ограждающей конструкции, Па; п – показатель степени, устанавливаемый экспериментально. Расход воздуха через i-ую ограждающую конструкцию будет равен
- разность давлений воздуха на наружной и внутренней поверхностях ограждающей конструкции, Па; п – показатель степени, устанавливаемый экспериментально. Расход воздуха через i-ую ограждающую конструкцию будет равен 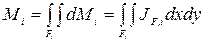 . Зависимость давления от высоты можно записать как dp=gpdz. Используя уравнение состояния
. Зависимость давления от высоты можно записать как dp=gpdz. Используя уравнение состояния 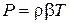 , получено уравнение:
, получено уравнение:
|
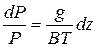
где
Р – давление, Па;
В - газовая постоянная для воздуха, Дж/(кг·К.);
Т - температура воздуха. К;
g - ускорение свободного падения, м/с2;
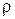 - плотность воздуха, кг/м3.
- плотность воздуха, кг/м3.
Интегрируя последнее уравнение, получено выражение:
|
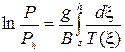
где
Р=Рz - давление на высоте z м, Па;
Ph - давление на высоте h м, Па.
Температуру воздуха 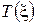 можно представить как
можно представить как 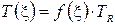 , где TR - температура воздуха в рабочей зоне помещения, К.
, где TR - температура воздуха в рабочей зоне помещения, К.
Применив к (2.1) теорему о среднем, получено выражение:
|
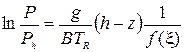
Здесь 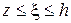 , поэтому можно обозначить как
, поэтому можно обозначить как 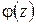 .
.
Вид функции 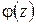 определяет характер распределения температуры воздуха по высоте помещения.
определяет характер распределения температуры воздуха по высоте помещения.
Последнее уравнение можно записать в виде:
|
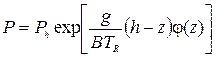
Величина показателя экспоненты будет равна:
g ~ 10; TR ~ 300K; (h-z) ~10; φ(z) ~ 1; B ~ 300
Тогда:
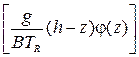 ~10-3
~10-3
Таким образом, с достаточной точностью для рассматриваемых процессов можно записать:
|
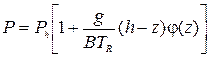
Для наружного воздуха можно считать 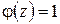 , если
, если 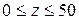 м. В этом случае наружное давление Р0 складывается из барометрического и давления, вызываемого ветровым напором:
м. В этом случае наружное давление Р0 складывается из барометрического и давления, вызываемого ветровым напором:
|
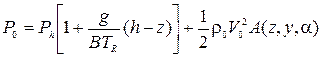
где
ρ0 - плотность наружного воздуха, кг/м3;
V0 - скорость ветра, м/с;
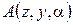 - функция аэродинамических коэффициентов здания.
- функция аэродинамических коэффициентов здания.
Подставляя соответствующие выражения в формулу расхода воздуха, получено выражение:
|
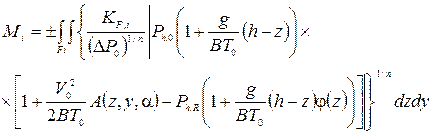
где
Ph.0 - наружное статическое давление на высоте h м, Па;
Ph.R - внутреннее статическое давление на высоте h м. Па.
Если воздух входит в помещение, то Мi>0, если выходит из помещения, то Mi<0.
Расчеты по формуле (2.10) дают возможность определять, до какой степени такие факторы, как давление, изменяются под действием ветра через поверхность ограждающих конструкций, а температура воздуха изменяется от высоты помещения (которыми, как правило, можно пренебрегать) влияют на определение количества инфильтрованного воздуха через ограждающие конструкции и, следовательно, определение теплопотерь и теплопоступлений помещения.
Учет изменения ветрового давления по площади ограждения и изменения температуры внутреннего воздуха по высоте помещения приводит к более точному определению расхода воздуха, фильтрующегося через ограждение, и, следовательно, к более правильному определению потерь тепла на инфильтрацию.
Граничное условие на внутренней поверхности ограждения включает количество тепла, передаваемого поверхностью теплопроводностью, количество тепла, воспринимаемого поверхностью в результате лучистого и конвективного теплообмена, источники тепла, обусловленные фазовыми переходами, и имеет вид:
|
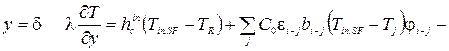
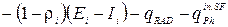
где
Tin.SF, Тj, ТR - соответственно, средняя температура внутренней поверхности ограждающей конструкции при рассмотрении внутренней поверхности j-oй ограждающей конструкции помещения и внутреннего воздуха, °С;
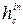 - коэффициент конвективного теплообмена между внутренней поверхностью ограждения и омывающим ее воздухом, Вт/(м°С);
- коэффициент конвективного теплообмена между внутренней поверхностью ограждения и омывающим ее воздухом, Вт/(м°С);
qRAD - поверхностная мощность источников тепла, обусловленных воздействием лучистого теплообмена между внутренней поверхностью ограждения и источником тепла в помещении, Вт/м2;
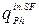 - источники тепла на поверхности, обусловленные фазовыми переходами, Вт/м2.
- источники тепла на поверхности, обусловленные фазовыми переходами, Вт/м2.
Перепишем последнее уравнение как:
|
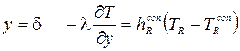
где
|
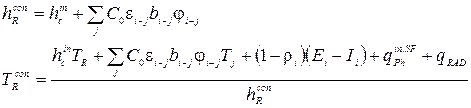
Граничное условие на наружной поверхности ограждения (2.14) включает количество тепла, передаваемое поверхностью теплопроводностью (qT), количество тепла, воспринимаемое поверхностью в результате конвективного теплообмена с наружным воздухом (qс), лучистого теплообмена с «окружением» (qsur), а также источники тепла, обусловленные солнечной радиацией, поглощенной поверхностью (qsol), и фазовыми переходами на поверхности ( 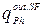 ).
).
|
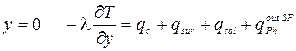
Величину qс, Вт/м2, рассчитывают по формуле:
|
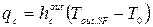
где
Т0, Tout.SF - соответственно температуры наружного воздуха и наружной поверхности ограждения, °С;
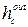 - коэффициент конвективного теплообмена между наружной поверхностью ограждения и омывающим ее потоком воздуха, Вт/(м·°С).
- коэффициент конвективного теплообмена между наружной поверхностью ограждения и омывающим ее потоком воздуха, Вт/(м·°С).
Величину qsur, Вт/м2, можно рассчитать по формуле:
|
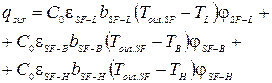
где
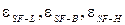 - приведенные коэффициенты излучения соответственно между ограждением и поверхностью земли, между ограждением и близ расположенными зданиями и сооружениями, между ограждением и «небом»;
- приведенные коэффициенты излучения соответственно между ограждением и поверхностью земли, между ограждением и близ расположенными зданиями и сооружениями, между ограждением и «небом»;
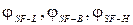 - коэффициенты облученности соответственно между ограждением и землей, между ограждением и близ расположенными зданиями и сооружениями, между ограждением и «небом»;
- коэффициенты облученности соответственно между ограждением и землей, между ограждением и близ расположенными зданиями и сооружениями, между ограждением и «небом»;
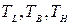 - температуры соответственно поверхности земли, близ расположенных зданий и сооружений, «неба», °С;
- температуры соответственно поверхности земли, близ расположенных зданий и сооружений, «неба», °С;
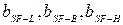 - корректирующие коэффициенты.
- корректирующие коэффициенты.
Таблица 2.1 - Значения температуры «неба» в зависимости от температуры наружного воздуха и парциального давления водяного пара у поверхности земли
| Температура наружного воздуха,°С | Значения температуры «неба» ТH, °С, при парциальном давлении водяного пара у поверхности земли, кПа | |||||||||||||
| 0,5 | 0,7 | 0,8 | 1,1 | 1,3 | 1,6 | 1,9 | 2,1 | 2,4 | 2,7 | 3,3 | 4,0 | 4,7 | 5,3 | |
| -25 | -23 | -21 | -17 | |||||||||||
| -18 | -14 | -12 | ||||||||||||
| -7 | -4 | -3 | ||||||||||||
| -1 | 1,5 | |||||||||||||
| 12,4 | 12,7 | |||||||||||||
| 17,4 | 17,7 |
Источник: Таблица 2.1 заимствована из источника /8/
При массовых расчетах с целью упрощения рекомендуется принимать:
- для холодного периода года:
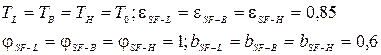
- для теплого периода года:
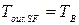 (лучистый теплообмен с близ расположенными зданиями не учитывается)
(лучистый теплообмен с близ расположенными зданиями не учитывается)
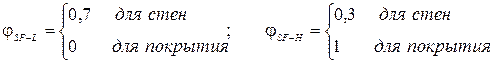
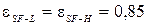
Летом температура «неба» может существенно отличаться от температуры наружного воздуха. Значения температуры безоблачного «неба» в дневное и ночное время в зависимости от парциального давления водяных паров у поверхности земли рекомендуется принимать по таблице 2.1.
Величина qsol, Вт1м2 , определяется по формуле:
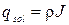
где ρ - коэффициент поглощения общей солнечной радиации материалом внутренней поверхности ограждения;
J - общая случайная солнечная радиации на внутреннюю поверхность, Вт/м2.
Уравнение (2.11) можно перписать в виде:
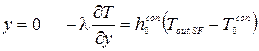
где 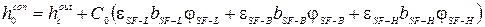
 3 ОСНОВНЫЕ ТРЕБОВАНИЯ К ТЕПЛОФИЗИЧЕСКИМ СВОЙСТВАМ ОГРАЖДАЮЩИХ КОНСТРУКЦИЙ ЗДАНИЙ
3 ОСНОВНЫЕ ТРЕБОВАНИЯ К ТЕПЛОФИЗИЧЕСКИМ СВОЙСТВАМ ОГРАЖДАЮЩИХ КОНСТРУКЦИЙ ЗДАНИЙ
Дата добавления: 2015-04-21; просмотров: 2437;
