Основы общей теории поля напряжений и деформаций в сплошной среде
Если перейти от рассмотрения напряженно-деформированного состояния отдельной точки к рассмотрению состояния какого-либо тела, то прежде всего необходимо ввести новое понятие «перемещение». Под перемещением будем понимать изменение положения какой-либо фиксированной точки в пространстве только за счет деформирования тела. Поскольку перемещение есть вектор, его проекции на оси координат X, Y и Z соответственно и, v и w.
Связь между компонентами напряженно-деформированного состояния в отдельных точках и компонентами перемещений в сплошной среде устанавливается с помощью уравнений, в основе которых лежат выражения для компонентов перемещений двух бесконечно близких точек (рис. 2.2):
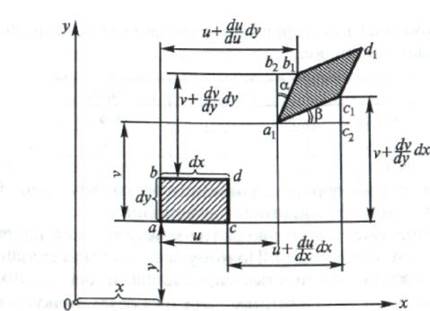
|

|
(2.3)
Однако, для того чтобы основное условие — сплошность среды — выполнялось и после деформирования, соотношение компонентов деформаций должно удовлетворять условиям неразрывности деформаций. Эти условия, называемые уравнениями Сен-Венана, непосредственно следуют из соотношений (2.2) и в прямоугольной системе координат имеют вид
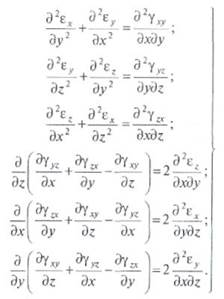 (2.4)
(2.4)
Таким образом, в соответствии с моделью сплошной среды для определения напряженно-деформированного состояния какого-либо тела имеется основная система из девяти независимых уравнений (2.3) и (2.4), в которых содержится 15 неизвестных: σх,σу, σz, τxy , τxz, τzy, εx, εy, γху, γyz, γzx, u, v, w.
Данные уравнения являются общими для любых моделей сплошной среды.
Однако в зависимости от конкретного вида применяемой модели сплошной среды, например упругой, пластической, вязкой и т. д., Для отражения особенностей деформирования вводится специальная группа уравнений, описывающая физические законы связи напряжений и деформаций.
Например, упругая модель основывается на прямой пропорциональности между напряжениями и деформациями — законе Гука.
При этом связь компонентов напряжений с компонентами деформаций — обобщенный закон упругости — может быть выражена следующими шестью уравнениями:
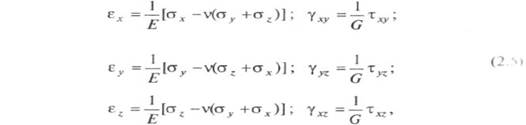
|
где Е — модуль упругости; С—модуль сдвига; v — коэффициент поперечных деформаций (коэффициент Пуассона).
Дополнением указанной группы уравнений к общей системе уравнений сплошной среды удается избавиться от статической не определенности, и число независимых уравнений становится равным числу неизвестных, которые таким образом могут быть найдены в ходе решения поставленных задач.
С точки зрения практических вопросов геомеханики большой интерес представляют частные случаи напряженно-деформированного состояния среды — плоское напряженное состояние и плоская деформация.
Плоское напряженное состояние возникает, когда все напряжения параллельны какой-либо одной плоскости (см. рис. 2.1.) Например, σz = 0; τzx = τzy = 0 и тензор напряжений имеет вид
| σх | τху |
| τух | σу |

| εz | 0,5уху | |
| 0,5γyx | εу | |
Плоское напряженное состояние характерно для объектов, у которых один из размеров существенно меньше двух других, например для тонких пластин, нагруженных по контуру силами, параллельными их плоскости. В частности, если в гравитационном сил в массиве пород вокруг вертикального ствола мысленно выделить тонкий слой, перпендикулярный его оси, то напряжение состояние пород в выделенном слое можно практически полагать плоским.
Условия плоской деформации возникают в случае, если перемещения точек деформируемого объема происходят только в одной плоскости, при этом εz = 0; yxz = 0; τyz = τxz = 0 и тензор деформации может быть записан в виде
| εх | 0,5γху |
| 0,5γух | εу |
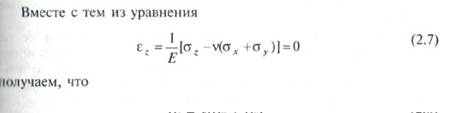
|
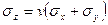 (2.8)
(2.8)
Таким образом, хотя εz = 0, тензор напряжений для условия плоской деформации содержит компоненту σг и имеет вид
| σх | τху | |
| τух | σу | |
| σz |
В состоянии плоской деформации находятся средние точки тела, размеры которого в одном каком-либо направлении очень велики, при условии, что не изменяющиеся по значению нагрузки действуют перпендикулярно этой длинной оси. Например, в гравитационном поле сил в условиях плоской деформации фактически находятся породы вокруг продольного сечения горизонтальной горной выработки.
Дата добавления: 2015-04-03; просмотров: 1379;
