Лекция 10.
Электронные состояния и электронно-колебательно-вращательные спектры молекул (УФ). Спектры двухатомных молекул. Классификация электронных состояний и разрешенные переходы. Колебательная структура. Таблица и серии Деландра. Принцип Франка-Кондона. Определение энергии диссоциации. Вращательная структура.
Классификация электронных состояний двухатомных молекул по проекции орбитального момента количества движения.
Эта классификация основана на следующем.
Орбитальный момент. Квадрат суммарного вектора L момента количества движения всех электронов молекулы определяется выражением:
L2 = 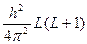
где L – соответствующее квантовое число.
Каждое электронное состояние двухатомной молекулы характеризуется определенным значением проекции орбитального момента количества движения на линию, соединяющую ядра молекулы. Эта проекция выражается в виде:
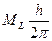
где 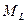 - квантовое число проекции орбитального момента – может быть равно одному из чисел :
- квантовое число проекции орбитального момента – может быть равно одному из чисел : 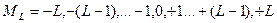
Состояния, отличающиеся только знаком 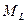 , не различаются по энергии. Различия в энергии определяются числом
, не различаются по энергии. Различия в энергии определяются числом 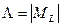 . Ряд других свойств состояний также определяются числом
. Ряд других свойств состояний также определяются числом 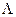 , поэтому электронные состояния классифицируют по значению этого числа:
, поэтому электронные состояния классифицируют по значению этого числа:
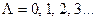
соответствуют символам
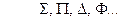
Магнитное поле, связанное с орбитальным моментов электронов, определяется проекцией орбитального момента на межъядерную ось, т.е. определяется квантовым числом 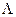 и направлено вдоль межъядерной оси.
и направлено вдоль межъядерной оси.
Для 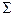 -состояний напряженность магнитного поля равна 0, для других – пропорциональна числу
-состояний напряженность магнитного поля равна 0, для других – пропорциональна числу 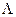 .
.
Спин, компонеты мультиплета. Квадрат вектора суммарного спина всех электронов 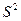 определяется квантовым числом
определяется квантовым числом 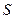 суммарного спина.
суммарного спина.
S2 = 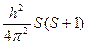
Квантовое число 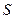 может быть целым (при четном количестве электронов) и полуцелым (при нечетном количестве электронов). Проекция суммарного вектора на межъядерную ось будет
может быть целым (при четном количестве электронов) и полуцелым (при нечетном количестве электронов). Проекция суммарного вектора на межъядерную ось будет
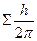
где 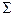 - квантовое число проекции суммарного спина – может быть равно одному из чисел :
- квантовое число проекции суммарного спина – может быть равно одному из чисел : 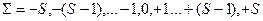 ( не путать с
( не путать с 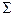 , определяющим квантовое состояние
, определяющим квантовое состояние 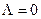 ).
).
Совокупность 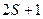 состояний, имеющих одно и тоже значение
состояний, имеющих одно и тоже значение 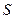 и разные значения
и разные значения 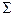 , называется мультиплетом, а отдельные состояния – компонентами мультиплета. Энергия компонента мультиплета определяется напряженностью внутреннего магнитного поля молекулы, пропорциональной
, называется мультиплетом, а отдельные состояния – компонентами мультиплета. Энергия компонента мультиплета определяется напряженностью внутреннего магнитного поля молекулы, пропорциональной 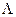 , и проекцией
, и проекцией 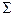 суммарного вектора спина на межъядерную ось. Если обозначить среднюю энергию мультиплета через
суммарного вектора спина на межъядерную ось. Если обозначить среднюю энергию мультиплета через 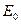 , то энергии отдельных его компонент может быть выражена:
, то энергии отдельных его компонент может быть выражена:
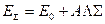
Например, для состояния 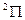 (
( 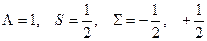 ):
):
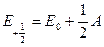
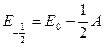
Каждый компонент мультиплета может быть охарактеризован суммарной проекцией орбитального и спинового моментов на межъядерную ось. Квантовое число этой проекции равно 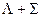 . Отдельные компоненты мультиплета обозначаются символом состояния и значением
. Отдельные компоненты мультиплета обозначаются символом состояния и значением 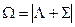 , которое ставится как нижний индекс справа. В примере
, которое ставится как нижний индекс справа. В примере
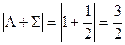
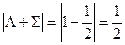
И компоненты дублета будут обозначаться как 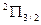 и
и 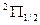 .
.
Дата добавления: 2015-04-19; просмотров: 1170;
