Политропический процесс

Политропическим процессом называется всякий процесс изменения состояния, при котором теплоёмкость газа С остаётся постоянной и равной .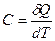

Отсюда выразим количество теплоты через теплоёмкость газа при политропическом процессе: 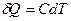. Используем первое начало термодинамики: 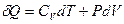. Здесь 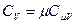и - теплоёмкости газа при постоянном объёме и давлении соответственно. С учётом выражения количества теплоты через теплоёмкость политропического процесса получим 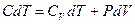или

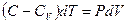(9-30)

Продифференцируем уравнение состояния идеального газа и выразим дифференциал температуры: 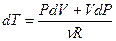. Учтём, что 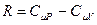, а , получим:

(9-31)

Обозначим - показатель политропы. После интегрирования (9-31) и дальнейшего потенцирования полученного результата, придём к уравнению политропы:

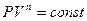(9-32)

Это уравнение может быть выражено и через другие пары параметров состояния, аналогично тому, как это было сделано для адиабатного процесса.

Рассмотренные изопроцессы и адиабатный процесс изменения состояния газа можно рассматривать как частные случаи более общего политропического процесса. Покажем, что из уравнения (9-32) можно получить уравнения известных нам процессов.

Для адиабатного процесса , следовательно, теплоёмкость С этого процесса равна нулю, а показатель политропы равен показателю адиабаты 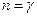. Тогда уравнение (9-32) перейдёт в уравнение адиабаты .

Для изотермического процесса dT=0 , , показатель адиабаты n=1 , а уравнение (9-32) перейдёт в уравнение изотермы: .

Для изобарного процесса С=С_Р , n=0 , а уравнение (9-32) будет иметь вид или Р=const .

Для изохорического процесса С=С_V , 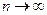, а уравнение (9-32) можно переписать в виде: . При 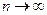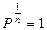, следовательно, уравнение (9-32) переходит в уравнение изохоры: V= const.