Уравнение процесса дросселирования

Пусть на участке трубопровода имеется суженное отверстие (см. рис. 14-1). Сечения I — I u II — II в трубопроводе закрыты невесомыми поршнями, которые могут перемещаться без трения. На поршень I площадью F₁ действует давление p₁ а на поршень II площадью f₂ действует давление р₂, причем р₁>р₂- Трубопровод не имеет теплообмена с внешней средой.

При перемещении 1 кг газа через отверстие поршень I перемес­тится в положение I', а поршень II — в положение II', при этом поршень I совершит путь s₁ а поршень II — путь s₂. Для пере­мещения 1 кг газа необходимо затратить работу p₁s₁F₁ или р₁v₁. Часть этой работы p₂F₂s₂ или p₂v₂ будет израсходована на преодоле­ние давления р₂, а разность работ p₁v₁ — p₂v₂ вызовет изменение энергии рабочего тела.

Если начальная скорость газа wi и внутренняя энергия и₁, конечная скорость w₂ и внутренняя энергия u₂. то будем иметь

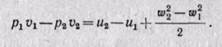
При условии, что скорости Wi и w₂ мало отличаются друг от друга, изменением внешней кинетической энергии можно пренебрегать и считать 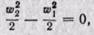отсюда

или

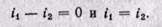(14-1)

Полученное равенство (14-1) показывает, что энтальпия в ре­зультате процесса дросселирования не изменяется. Этот вывод к промежуточным состояниям газа неприменим. В сечениях у от­верстия энтальпия не остается постоянной величиной, т. е. процесс дросселирования нельзя отождествлять с изоэнтальпическим процессом. Равенство (14-1) справедливо только для сечений, достаточно удаленных от сужения.

Выше указывалось, что энтальпия идеального газа является однозначной функцией температуры. Отсюда следует, что в резуль­тате дросселирования идеального газа температура его не изменяет­ся (Т₁ = T₂).

В результате процесса дросселирования реального газа энталь­пия для начальных и конечных значений остается одинаковой, энтро­пия и объем увеличиваются, давление падает, а температура может увеличиваться, уменьшаться или же, в частном случае, остаться без изменения.