Напряжения в круговых швах

Круговые швы применяются при вварке в лист круглых вставок, при сварке колес и т.д. Частными случаями кругового шва (рис. 32,а) являются прямой шов (при r_ш → ∞) и точечное соединение (при r_ш → 0).

Рис.32. Круговой шов в пластине: а – компоненты перемещений, б – равновесие напряжений

При сварке кругового шва происходит сложное взаимодействие продольной и поперечной усадки, характер которого зависит от радиуса шва r_ш. Если не рассматривать замковую часть, где встречаются начало и конец шва, то можно считать напряженно-деформированное состояние осесимметричным. Все точки перемещаются только по радиусам, перемещения вдоль окружности шва отсутствуют (u_t = 0, см. рис. 32,а). Перемещение по радиусу вызывает сразу 2 компоненты деформации:

радиальную (42)

и окружную 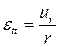. (43)

Радиальная деформация возникает, если 2 соседние точки отрезка радиуса имеют разные перемещения (если изменяется длина отрезка). Окружная деформация возникает при любых перемещениях, так как при изменении радиуса изменяется длина окружности.

Радиальные и окружные напряжения связаны уравнением равновесия. Рассмотрим полукольцо, вырезанное из пластины (рис. 32,б). Оно должно находиться в равновесии по оси y: ,

, где s – толщина пластины. Получаем

. (44)

Из уравнения следует, что в той зоне, где σ_tt > σ_rr, происходит рост σ_rr по мере роста r. Для упругой части пластины (при постоянной температуре и отсутствии пластической деформации) имеются уравнения, связывающие u_r,ε_rrиε_tt с r:

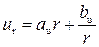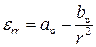, , (45)

где коэффициенты a_u и b_u должны быть найдены из граничных условий на наружной и внутренней границах этой части пластины. Аналогичные уравнения имеются для компонент напряжения:

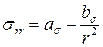, . (46)

Коэффициенты a_σ и b_σможно выразить через a_u и b_u и наоборот, если известны упругие характеристики материала.

В пластине с круговым швом можно выделить 3 зоны (рис. 33,а). Так же как при сварке прямолинейного шва, возникает зона пластических деформаций укорочения 2. Она имеет вид кольца шириной 2b_пл. Внутри и снаружи от нее располагаются зоны 1 и 3, в которых пластические деформации не происходят, поэтому в них распределения остаточных деформаций и напряжений описываются уравнениями (45, 46).

В зоне 1 b_u= 0, b_σ=0; 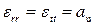, 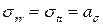(рис. 33, б). В зоне 3 a_u = 0, a_σ = 0; 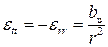, 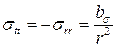. В пластической зоне 2 уравнения (45, 46) не действует, но соблюдается условие равновесия (44).

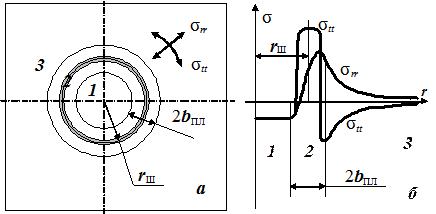
Рис.33. Остаточные напряжения при сварке кругового шва: а – зоны в сварном соединении, б – эпюры остаточных напряжений

На стадии нагрева металл зоны 2 расширяется в большей степени, чем в зонах 1 и 3. Увеличивается как ширина кольца, так и длина его окружности, а следовательно и радиус оси шва. При этом в металле зоны 2 возникают сжимающие окружные напряжения σ_tt<0, направленные вдоль оси шва. Эти напряжения достигают предела текучести, который в зоне 2 снижается при высокой температуре нагрева. Происходит пластическое продольное и поперечное сокращение зоны 2 (сокращение длины и ширины кольца), аналогичное сокращению при сварке прямолинейного шва, с увеличением толщины кольца (образуется выпуклость шва). При этом в зоне 3 снаружи от шва возникает сжатие в радиальном направлении и растяжение в окружном (σ_rr<0, σ_tt>0).

После остывания картина изменяется (см. рис. 33,б). В результате продольной и поперечной усадки кольцо пластической зоны 2 после остывания имеет меньший радиус и ширину, чем до сварки. В этой зоне возникают растягивающие окружные напряжения σ_tt, близкие к пределу текучести (аналогично продольным напряжениям в прямом шве). σ_rr в этой зоне растет при удалении от центра окружности шва в соответствии с формулой (44), так как σ_tt > σ_rr.

Снаружи от шва (в зоне 3) возникают растягивающие напряжения в радиальном направлении. Этому способствуют как продольная усадка (сокращение радиуса оси кольцевой зоны 2), так и поперечная (сокращение ширины кольца). В окружном направлении возникают сжимающие напряжения, равные по величине и противоположные по знаку радиальным напряжениям. Оба компонента убывают по мере удаления от шва.

Внутри окружности шва (в зоне 1) компоненты напряжения равны друг другу и постоянны (не зависят от координаты r). Их уровень и знак зависят от радиуса шва r_ш: при малых радиусах внутри круга растяжение, при больших – сжатие (рис.34). Это объясняется тем, что продольная усадка (сокращение радиуса шва) способствует сжатию зоны 1, а поперечная – ее растяжению и соотношение их влияния различно при разных радиусах шва.

Рис. 34. Остаточные напряжения при различных радиусах шва

По мере увеличения радиуса шва r_ш радиальные напряжения уменьшаются, а эпюра окружных приближается по виду к эпюре продольных напряжений у прямолинейного шва (см. рис. 8, 9).

Если диаметр шва становится меньше ширины пластической зоны, то распределение напряжений приобретает такой же вид, как при точечной контактной сварке. В этом случае в зоне 3 распределение остаточных напряжений такое же, как на рис. 33,б, а в зоне 1 оба компонента равны, положительны (растяжение) и близки к пределу текучести (зоны 1 и 2 сливаются).

Потеря устойчивости пластин под действием продольной усадки

В результате продольной усадки пластины, в активной зоне вблизи шва возникают остаточные напряжения растяжения, а в остальной части пластины – сжатия. Напряжения сжатия могут вызвать потерю устойчивости, в результате пластина изогнется и перестанет быть плоской. Рассмотрим причины потери устойчивости и формулы расчета условий ее появления.

При приложении к упругой балке поперечной силы P в ней возникнет прогиб f, пропорциональный P и зависящий от размеров и условий закрепления балки. Силу, вызывающую единичный прогиб, можно назвать жесткостью балки при изгибе .

Если теперь приложить к балке продольные растягивающие силы T, то от них возникает изгибающий момент, уменьшающий прогиб. Таким образом, растяжение увеличивает жесткость балки k. Наглядным примером может служить гибкий трос, который при сильном натяжении становится достаточно жестким, чтобы выдерживать вес вагонов канатной дороги. От приложения сжимающих сил прогиб увеличивается (рис. 35), а жесткость при изгибе снижается, так как момент от сил Tсуммируется с моментом от поперечной силы P.

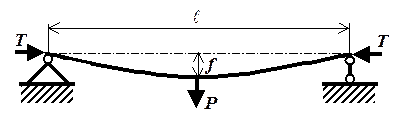
Рис.35. Изгиб балки под действием продольных и поперечных сил

При некотором значении сжимающей силы T_кр жесткость балки при изгибе снижается до нуля, то есть балка изгибается под действием продольных сил без приложения поперечной силы. Это явление называется потерей устойчивости, а сила T_кр – критической силой или силой Эйлера , где I - момент инерции сечения, а ℓ– длина полуволны изогнувшейся после потери устойчивости оси балки. Для балки с прямоугольным поперечным сечением критическое напряжение от продольных сжимающих сил , где h – высота сечения балки. Степень влияния продольной растягивающей или сжимающей силы на жесткость при изгибе зависит от отношения приложенной силы к критической T/T_кр.

Поперечное сечение балки при изгибе искажается и теряет прямоугольную форму вследствие поперечной деформации. Сжатая часть сечения становится шире, чем растянутая, а боковые стороны сечения наклоняются (рис. 36,а). Изгиб широкой пластины отличается от изгиба балки тем, что форма сечения искажается только у краев пластины, а в средней части продольные сечения остаются вертикальными (рис. 36,б). При этом в отличие от балки, в пластине возникают поперечные растягивающие и сжимающие напряжения.

Рис.36. Поперечные сечения балки (а) и пластины (б) при изгибе (стрелками показаны напряжения, обеспечивающие сохранение формы сечения пластины)

Это несколько повышает жесткость при изгибе и критическое продольное напряжение , где s – толщина пластины. Условия закрепления и приложения сжимающих сил влияют на длину полуволны изгиба ℓ, а также могут привести к сложному изгибу в двух направлениях. Общая формула для критических напряжений в закрепленной пластине

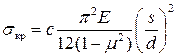, (47)

где d – один из размеров пластины. Как правило, d – меньший из двух размеров пластины, так как он обычно сильнее влияет на ее жесткость. Влияние второго из размеров, а также условий закрепления пластины и приложения сжимающей нагрузки отражает безразмерный коэффициент c. Если один из размеров существенно превышает длину полуволны ℓ изгиба пластины после потери устойчивости, то его дальнейшее увеличение практически не влияет на жесткость пластины и критическое напряжение.

Для расчета на устойчивость необходимо определить действующие в пластине напряжения и сопоставить их с критическими. Иногда потеря устойчивости происходит не после сварки, а при работе сварной конструкции. В этом случае при расчете напряжений следует, кроме сварочных остаточных напряжений, учесть напряжения от рабочих нагрузок. Рассмотрим несколько примеров потери устойчивости.

1) При изготовлении сварных профилей (тавров, двутавров и т.д.) возникают усадочные силы от продольных (поясных) швов. Значения этих сил можно найти по формулам (9, 10, 13) и затем по формуле (12) определить напряжение в любой точке пассивной части сечения. Максимальное сжимающее напряжение в каждой из пластин, из которых состоит сечение, нужно сопоставить с критическим напряжением для этой пластины.

Стенка двутаврового профиля приварена к полкам, поэтому она представляет собой пластину с закрепленными краями (рис. 37,а). Для такой пластины в формуле (47) в качестве размера d следует подставлять ее ширину d = H (см. рис. 37). Если жесткость полок достаточна, чтобы предотвратить поворот краев стенки вокруг продольной оси (заделка), а длина профиля в несколько раз превышает Н, то середина стенки после потери устойчивости изгибается по синусоиде с длиной полуволны ℓ ≈ 0,66·H. При этом в формуле (47) c ≈ 7. Если же полки не препятствуют повороту (шарнирная опора), то ℓ ≈ H, а c ≈ 4. На практике имеет место нечто среднее между этими двумя случаями, тогда 0,66H < ℓ < H; 4 < c < 7. При расчете приходится выбирать расчетную схему, исходя из соотношения размеров стенки и полки. Обычно полки двутавра толще, чем стенки, что дает основания считать закрепление близким к заделке. С другой стороны, для консервативной оценки (с запасом) нужно принимать наименьшее из возможных значений коэффициента.

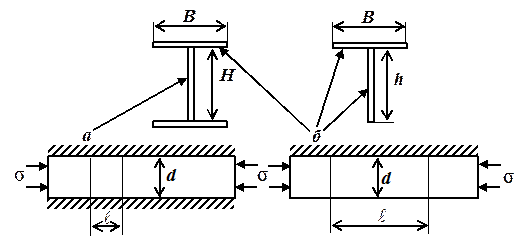
Рис.37. Схема расчета на устойчивость элементов сечения двутавра и тавра

Стенка таврового профиля, а также половина полки тавра или двутавра представляет собой пластину, один край которой закреплен, а другой свободен и может изгибаться (рис. 37,б). Для такой пластины в формуле (47) в качестве размера d следует подставлять ширину стенки d = h или половину ширины полки d = B/2 (см. рис. 37). Для длинного профиля при отсутствии поворота закрепленного края ℓ ≈ 1,64 d, а c ≈ 1,3. При шарнирном закреплении образуется одна полуволна, длина ℓ которой равна длине профиля, а c ≈ 0,43. Эти цифры показывают, насколько сильно закрепления краев пластины влияют на ее жесткость и устойчивость.

При промежуточных схемах закрепления 0,43 < c < 1,3.

2) При приварке плоского днища к цилиндрическому сосуду в результате продольной усадки на контуре круглой пластины (днища) действуют радиальные сжимающие остаточные напряжения σ_rr (см. рис. 33). Их можно вычислить, если известна усадочная сила в круговом шве: . Для этого случая в формуле (47) в качестве размера d следует подставлять радиус шва d = r_ш, а c ≈ 1,5, если контур пластины закреплен жестко (например, днище приварено к жесткому фланцу), и c ≈ 0,43, если закрепление шарнирное. При промежуточных схемах закрепления 0,43 < c < 1,5.

Перемещения листовых конструкций после потери устойчивости

После потери устойчивости начинаются значительные перемещения, изменяющие форму и размеры конструкции, и расчет этих перемещений является весьма сложной задачей. Сравнительно простое решение этой задачи возможно в том случае, когда только один из элементов сечения (наиболее гибкий) теряет устойчивость.

При расчете принимаются следующие допущения.

1) До потери устойчивости все элементы сечения работают упруго.

2) Потеря устойчивости в одном из элементов происходит, когда действующие в нем напряжения достигают критического уровня , который может быть найден по формуле (47). Одновременно необходимо определить длину полуволны изгиба ℓ.

Например, если профиль таврового сечения длиной L (рис. 38) состоит из двух элементов (полки и стенки), поперечные сечения которых A₁ и A₂, и элемент A₁ теряет устойчивость, то сжимающее напряжение в нем равно , а длина полуволны изгиба ℓ ≈ 1,64· d. Если потеря устойчивости произошла под действием продольной сжимающей силы P (изгиб отсутствует), то напряжение во всем поперечном сечении одинаковое. Можно вычислить критическую силу: 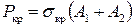и ее часть, приходящуюся на элемент A₁: .

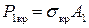Рис. 38. Перемещения w₁ стенки таврового профиля после потери устойчивости под действием продольных сжимающих сил P

3) После потери устойчивости элемента A₁, элемент A₂ остается прямым (его прогиб ) и при дальнейшем росте сжимающей силы P деформируется упруго, по закону Гука. Сокращение длины всего профиля равно сокращению элемента A₂: , где - часть силы P, приходящаяся на элемент A₂.

4) Часть сжимающей силы P, воспринимаемая элементом A₁ после потери устойчивости, остается постоянной . Элемент A₁ перестает сокращаться в длину, только изгибается 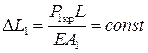. При дальнейшем сжатии увеличивается прогиб этого элемента w₁. Суммарная сила, воспринимаемая профилем, растет только за счет роста P₂.

Характер изменения сил, воспринимаемых элементами сечения, и прогибов этих элементов показан на рис. 39. На рис. 38 показан вид таврового профиля после потери устойчивости стенки. Чем больше разница укорочения стенки 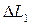и полки 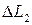, тем больше перемещения стенки .

Рис. 39. Характер изменения сил и прогиба элементов сечения (сплошными линиями показаны реальные зависимости, пунктиром - согласно сделанным допущениям)

Для того чтобы найти максимальное перемещение w_1max (прогиб), нужно задать уравнение линии изгиба. На рис. 38 видно, что эта линия близка к синусоиде 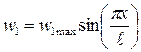. Соотношение длины полуволны синусоиды к длине хорды, соединяющей ее концы, может быть найдено интегрированием: , откуда получаем

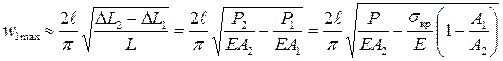. (48)