Генетическое разнообразие

Естественное богатство нашей планеты связано с разнообразием генетических вариаций. Генетическое разнообразие, т. е. поддержание генотипических гетерозиготности, полиморфизма и другой генотипической изменчивости, которая вызвана адаптационной необходимостью в природных популяциях, представлено наследуемым разнообразием внутри и между популяциями организмов.

Как известно, генетическое разнообразие определяется варьированием последовательностей 4 комплиментарных нуклеотидов в нуклеиновых кислотах, составляющих генетический код. Каждый вид несет в себе огромное количество генетической информации: ДНК бактерии содержит около 1 000 генов, грибы – до 10 000, высшие растения – до 400 000. Огромно количество генов у многих цветковых растений и высших таксонов животных. Например, ДНК человека содержит более 30 тыс. генов.

Новые генетические вариации возникают у особей через генные и хромосомные мутации, а также у организмов, которым свойственно половое размножение, через рекомбинацию генов. Генетические вариации могут быть оценены у любых организмов, от растений до человека, как число возможных комбинаций различных форм от каждой генной последовательности. Другие разновидности генетического разнообразия, например количество ДНК на клетку, структура и число хромосом, могут быть определены на всех уровнях организации живого.

Огромное множество генетических вариаций представлено у скрещивающихся популяций и может быть осуществлено посредством селекции. Различная жизнеспособность отражается в изменениях частот генов в генофонде и является реальным отражением эволюции. Значение генетических вариаций очевидно: они дают возможность осуществления и эволюционных изменений и, если это необходимо, искусственного отбора.

Только небольшая часть (около 1%) генетического материала высших организмов изучена в достаточной мере, когда мы можем знать, какие гены отвечают за определенные проявления фенотипа организмов. Для большей части ДНК ее значение для вариации жизненных форм остается неизвестным.

Каждый из 10⁹ различных генов, распределенных в мировой биоте, не дает идентичного вклада в формирование разнообразия. В частности, гены, контролирующие фундаментальные биохимические процессы, являются строго консервативными у различных таксонов и, в основном, демонстрируют слабую вариабельность, которая сильно связана с жизнеспособностью организмов.

Если судить об утере генофонда с точки зрения генной инженерии, принимая во внимание то, что каждая форма жизни уникальна, вымирание всего лишь одного дикого вида означает безвозвратную потерю от тысячи до сотен тысяч генов с неизвестными потенциальными свойствами. Генная инженерия могла бы использовать это разнообразие для развития медицины и создания новых пищевых ресурсов. Однако разрушение местообитаний и ограничение размножения многих видов приводит к опасному уменьшению генетической изменчивости, сокращая их способности адаптироваться к загрязнению, изменениям климата, болезням и другим неблагоприятным факторам. Основной резервуар генетических ресурсов – природные экосистемы – оказался значительно измененным или разрушенным. Уменьшение генотипического разнообразия, происходящее под воздействием человека, ставит на грань риска возможность будущих адаптаций в экосистемах.

Изучение закономерностей распределения генотипов в популяциях начато Пирсоном [1904]. Он показал, что при наличии разных аллелей одного гена и действия свободного скрещивания в популяциях возникает совершенно определенное распределение генотипов, которое можно представить в виде:

,

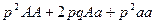где p – концентрация гена A; q – концентрация гена a.

Х. Харди (1908) и В. Вайнберг (1908), специально исследовав это распределение, высказали мнение, что оно является равновесным, так как при отсутствии факторов, нарушающих его, оно может сохраняться в популяциях неограниченное время. Так стала развиваться популяционная генетика. Главная заслуга в разработке популяционной генетики, а особенно ее теоретического и математического аспектов, в этот ранний период [1920–1940 гг.] принадлежит С. С. Четверикову, С. Райту, Р. Фишеру, Дж. Холдейну, А. С. Серебровскому и Н. П. Дубинину.

Биологическая эволюция – это процесс накопления изменений в организмах и увеличение их разнообразия во времени. Эволюционные изменения затрагивают все стороны существования живых организмов: их морфологию, физиологию, поведение и экологию. В основе всех этих изменений лежат генетические изменения, т.е. изменения наследственного вещества, которое, взаимодействуя со средой, определяет все признаки организмов. На генетическом уровне эволюция представляет собой накопление изменений в генетической структуре популяций.

Эволюцию на генетическом уровне можно рассматривать как двухступенчатый процесс. С одной стороны, возникают мутации и рекомбинации – процессы, обусловливающие генетическую изменчивость; с другой стороны, наблюдается дрейф генов и естественный отбор – процессы, посредством которых генетическая изменчивость передается из поколения в поколение.

Эволюция возможна только в том случае, если существует наследственная изменчивость. Единственным поставщиком новых генетических вариантов служит мутационный процесс, однако эти варианты могут по-новому рекомбинироваться в процессе полового размножения, т. е. при независимом расхождении хромосом и вследствие кроссинговера. Генетические варианты, возникшие в результате мутационного и рекомбинационного процессов, передаются из поколения в поколение отнюдь не с равным успехом: частота некоторых из них может увеличиваться за счет других. Помимо мутаций к процессам, изменяющим частоты аллелей в популяции, относится естественный отбор, поток генов (т. е. миграции их) между популяциями и случайный дрейф генов.

На первый взгляд может показаться, что особи с доминантным фенотипом должны встречаться чаще, чем с рецессивным. Однако соотношение 3:1 соблюдается лишь в потомстве двух особей, гетерозиготных по одним и тем же двум аллелям. При других типах скрещивания в потомстве происходит иное расщепление признаков, и такие скрещивания также влияют на частоты генотипов в популяции. Законы Менделя ничего не говорят нам о частотах генотипов в популяциях. Именно об этих частотах идет речь в законе Харди – Вайнберга. Основное утверждение закона Харди – Вайнберга состоит в том, что в отсутствие элементарных эволюционных процессов, а именно мутаций, отбора, миграции и дрейфа генов, частоты генов остаются неизменными из поколения в поколение. Этот закон утверждает также: если скрещивание случайно, то частоты генотипов связаны с частотами генов простыми (квадратичными) соотношениями. Из закона Харди – Вайнберга вытекает следующий вывод: если частоты аллелей у самцов и самок исходно одинаковы, то при случайном скрещивании равновесные частоты генотипов в любом локусе достигаются за одно поколение. Если частоты аллелей у двух полов исходно различны, то для аутосомных локусов они становятся одинаковыми в следующем поколении, поскольку и самцы, и самки получают половину своих генов от отца и половину – от матери. Таким образом, равновесные частоты генотипов достигаются в этом случае за два поколения. Однако в случае сцепленных с полом локусов равновесные частоты достигаются лишь постепенно.

Закон Харди – Вайнберга сформулировали в 1908 году независимо друг от друга математик Г. Х. Харди в Англии и врач В. Вайнберг в Германии. Чтобы понять смысл этого закона, можно привести следующий простой пример. Предположим, что данный локус содержит один из двух аллелей, A и a, представленных с одинаковыми для самцов и самок частотами: p для A и q для a. Представим себе, что самцы и самки скрещиваются случайнымобразом, или, что то же самое, гаметы самцов и самок образуют зиготы, встречаясь случайно. Тогда частота любого генотипа будет равна произведению частот соответствующих аллелей. Вероятность того, что некоторая определенная особь обладает генотипом AA, равна вероятности (p) получить аллель A от матери, умноженной на вероятность (p) получить аллель A от отца, т. е. .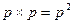

Закон Харди – Вайнберга гласит, что процесс наследования преемственности сам по себе не ведет к изменению частот аллелей и (при случайном скрещивании) частот генотипов по определенному локусу. Более того, при случайном скрещивании равновесные частоты генотипов по данному локусу достигаются за одно поколение, если исходные частоты аллелей одинаковы у обоих полов.

Равновесные частоты генотипов задаются произведениями частот соответствующих аллелей. Если имеются только два аллеля, A и a, с частотами p и q, то частоты всех трех возможных генотипов выражаются уравнением:

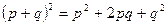
A a AA Aa aa,

где буквам во второй строке, обозначающим аллели и генотипы, соответствуют расположенные над ними частоты в первой строке.

Если имеется три аллеля, скажем, A₁, A₂ и A₃ , с частотами p, q и r, то частоты генотипов определяются следующим образом:

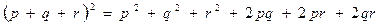
A1 A2 A3 A1A1 A2A2 A3A3 A1A2, A1A3 A2A3.

Аналогичный прием возведения в квадрат многочлена может быть использован для определения равновесных частот генотипов при любом числе аллелей. Заметим, что сумма всех частот аллелей так же как и сумма всех частот генотипов, должна быть равна единице. Если имеются только два аллеля с частотами p и q, то p + q = 1, и, следовательно, 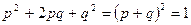; если же имеются три аллеля с частотами p, q и r, то p + q + r = 1, и, следовательно, также 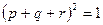и т. д.

Организмы, обладающие удачными вариантами признаков, имеют большую вероятность по сравнению с другими организмами выжить и оставить потомство. Вследствие этого полезные вариации в ряду поколений будут накапливаться, а вредные или менее полезные вытесняться, элиминироваться. Это и называется процессом естественного отбора, который играет ведущую роль в определении направления и скорости эволюции.

Прямая взаимосвязь между степенью генетической изменчивости в популяции и скоростью эволюции под действием естественного отбора была доказана математическим путем Р. Фишером [1930] в его фундаментальной теореме естественного отбора. Фишер ввел понятие приспособленности и доказал, что скорость возрастания приспособленности популяции в любой момент времени равна генетической вариансе приспособленности в тот же момент времени. Однако прямые доказательства этого факта были получены лишь в конце 60-х годов ХХ столетия.

Мутационный процесс служит источником появления новых мутантных аллелей и перестроек генетического материала. Однако возрастание их частоты в популяции под действием мутационного давления происходит крайне медленно, даже в эволюционном масштабе. К тому же подавляющее большинство возникающих мутаций устраняются из популяции в течение немногих поколений уже в силу случайных причин. Неизбежность такого течения событий впервые обосновал Р. Фишер в 1930 году.

Для человека и других многоклеточных показано, что мутации обычно возникают с частотой от 1 на 100 000 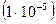до 1 на 1 000 000 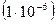гамет.

Новые мутанты, хотя и довольно редко, но постоянно появляются в природе, поскольку существует множество особей каждого вида и множество локусов в генотипе любого организма. Например, число особей того или иного вида насекомых обычно составляет около 100 млн. (10⁸). Если предположить, что средняя мутабельность по одному локусу равна 1 мутации на 100 000 (10^-5) гамет, то среднее число вновь возникающих в каждом поколении мутантов по этому локусу для данного вида насекомых составит 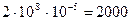. (Частота возникновения мутаций умножается на число особей и еще на два, так как любая особь представляет собой продукт слияния двух гамет.) В генотипе человека имеется около 100 000 (10⁵) локусов. Предположим, что у человека темп мутирования такой же, как у дрозофилы; в этом случае вероятность того, что генотип каждого человека содержит новый аллель, отсутствовавший в генотипе его родителей, равна 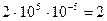. Иными словами, каждый человек в среднем несет около двух новых мутаций.

Проделанные выше расчеты основаны на частотах возникновения мутаций, обладающих внешним проявлением. В целом по геному темп мутирования составляет не менее 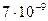замен на одну нуклеотидную пару в год. У млекопитающих число нуклеотидных пар в диплоидном геноме составляет около 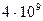. Следовательно, нуклеотидные замены у млекопитающих происходят с частотой не менее 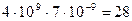в год на диплоидный геном. Ясно, что мутационный процесс обладает колоссальными возможностями поставлять новый наследственный материал.

Важный шаг в генетике популяций был сделан в 1926 году С. С. Четвериковым. Исходя из закона Харди – Вайнберга, С. С. Четвериков доказал неизбежность генетической разнородности природных популяций при том, что новые мутации непрерывно появляются, но остаются обычно скрытыми (рецессивными), а в популяции идет свободное скрещивание.

Из расчетов Четверикова следовало, а впоследствии это было полностью подтверждено практикой, что даже редкие и вредные для особи мутантные гены будут надежно укрыты от очищающего действия естественного отбора в гетерозиготах (организмах со смешанной наследственностью) с доминирующими безвредными генами нормального дикого типа. Это значит, что даже вредная гетерозигота (организм с однородной наследственностью) мутация будет сохраняться в виде генетической «примеси» в течение ряда поколений. Мутация будет как бы поглощена популяцией, из-за чего за внешним однообразием особей одной популяции неизбежно скрывается их огромная генетическая разнородность. Четвериков это выразил так: «Вид, как губка, впитывает в себя гетерозиготные геновариации, сам оставаясь при этом все время внешне (фенотипически) однородным». Для жизни популяций эта особенность может иметь два разных следствия. В огромном большинстве случаев при изменении условий среды вид может реализовать свой «мобилизационный резерв» генетической изменчивости не только за счет новых наследственных изменений у каждой особи, но и благодаря «генетическому капиталу», доставшемуся от предков. Благодаря такому механизму наследования популяция приобретает пластичность, без чего невозможно обеспечить устойчивость приспособлений в меняющихся условиях среды. Однако изредка возможен и другой исход: редкие скрытые вредные мутации иногда могут встретиться у потомства совершенно здоровых родителей, приводя к появлению особей с наследственными заболеваниями. И это – тоже закономерное, неистребимое биологическое явление, своего рода жестокая плата популяции за поддержание своей наследственной неоднородности.

С. С. Четверикову популяционная генетика обязана еще одним открытием, которое было изложено в маленькой, всего на 4 страницы, заметке «Волны жизни», опубликованной в 1905 году на страницах «Дневника Зоологического отделения Императорского общества любителей естествознания и этнографии» в Петербурге. Он обратил внимание, что поскольку любая природная популяция имеет конечную, ограниченную численность особей, это неизбежно приведет к чисто случайным статистическим процессам в распространении мутаций. При этом популяции всех видов постоянно меняют численность (численность грызунов в лесу может от года к году изменяться в сотни, а многих видов насекомых – в десятки тысяч раз), из-за чего в разные годы распространение мутаций в популяциях может идти совершенно по-разному. От громадной популяции птиц, насекомых, зайцев и других животных в трудный для переживания год может остаться всего несколько особей, причем иногда совершенно нетипичных для бывшей популяции. Но именно они дадут потомство и передадут ему свой генофонд, так что новая популяция по составу генетического материала будет совершенно иной, чем прежняя. В этом проявляется генетический «эффект основателя» популяции. Постоянно изменяется и геном в популяциях человека. К. Альстрем на материале в южной Швеции показал, что в популяции человека передается следующему поколению далеко не весь имеющийся генофонд, а лишь избранная, а то и случайно «выхваченная» часть. Так, 20% поколения здесь вовсе не оставили потомков, зато 25% родителей, которые имели трех и более детей, дали 55% численности следующего поколения.

Постоянное давление мутаций и миграции генов, а также выщепление биологически менее приспособленных генотипов по сбалансированным полиморфных локусам создает проблему так называемого генетического груза.

Понятие генетического груза ввел Г. Меллер в 1950 году в работе «Наш груз мутаций». По его расчетам, от 10 до 50% гамет у человека содержат хотя бы одну вновь возникшую мутацию. Слабо вредящие мутации, если только они проявляются в гетерозиготе, способны нанести популяции больший урон, чем полностью рецессивные летальные мутации. Каждый из нас является носителем по крайней мере восьми вредных мутаций, скрытых в гетерозиготном состоянии. Г. Мёллер в соавторстве с Н. Мортоном и Дж. Кроу [1956] произвели оценку генетического груза мутаций путем сравнения детской смертности в случайных выборках из популяций и в семьях, где имели место браки между родственниками. Они выделили собственно мутационный груз, возникающий в результате мутационного давления, и сегрегационный груз как следствие расщепления. Ими предложены расчеты летального эквивалента, соответствующего числу мутаций, дающих вместе летальный исход. Так, один летальный эквивалент может соответствовать одной летальной мутации, двум полулетальным и т. д. Было показано, что средняя величина генетического груза у человека равна 3–5 летальным эквивалентам.

Ю. П. Алтухов с коллективом сотрудников [1989] в результате длительного изучения локальных стад рыб – больших изолированных друг от друга популяций с исторически сложившейся субпопуляционной структурой – пришел к выводу о высокой их устойчивости во времени и пространстве. Изменчивость на уровне отдельных субпопуляций не играет самостоятельной роли и отражает локальные различия действия отбора в силу гетерогенности условий обитания, а также влияние случайных факторов. К аналогичному заключению еще раньше пришел Ю. Г. Рычков при исследовании с сотрудниками изолированных групп популяций человека – коренного населения циркумполярной зоны Евразии. Американский генетик и селекционер И. М. Лернер еще в 1954 году выдвинул представление о генетическом гомеостазе, определив его как способность популяции приводить в равновесие свою генетическую структуру и противостоять внезапным изменениям. Один из важных механизмов генетического гомеостаза – отбор в пользу гетерозигот, ведущий к сбалансированному равновесию. Вместе с тем этот же механизм служит причиной образования генетического груза – выщепляющихся гомозиготных классов особей. Такой груз был назван сбалансированным и рассматривается как плата за поддержание гетерозигот, причисленных к генетической элите популяции.

Частоты генов в популяциях. Для описания ситуаций в популяционной генетике создано несколько математических моделей. Важнейшая заслуга в разработке этой области принадлежит Сьюэллу Райту. Еще в 1928 году Валунд [Wahlund, 1928] установил, что если большая популяция подразделена на K панмиктических групп, то в такой совокупности наблюдается эффект, подобный последствиям инбридинга в неподразделенной популяции: доля гомозигот возрастает на величину межпопуляционной вариансы частот генов за счет уменьшения доли гетерозигот.

Принципиальный вклад в описание локальной дифференциации частот генов в подразделенной популяции в терминах F - статистики был внесен С. Райтом [1943, 1951], который обосновал несколько F - коэффициентов как показателей меры генетической дифференциации:

1) F_IT – коэффициент инбридинга особи относительно целой (T) популяции;

2) F_IS – коэффициент инбридинга особи относительно субпопуляции (S);

3) F_ST – коэффициент инбридинга субпопуляции относительно всей подразделенной популяции.

Соотношение между этими величинами задается равенством:

.

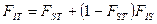Коэффициент F_ST был предложен С. Райтом еще в 1943 году и с тех пор неоднократно использовался при анализе распределений частот генов в природных подразделенных популяциях. Коэффициент Райта представляет большой интерес, так как позволяет вычленить некоторые важные влияния популяционной подразделенности на генетическую структуру. Для этой цели С. Райт предложил две оригинальные модели популяций: «островная модель» и «изоляция расстоянием».

Островная модель. Известны для варианта островной модели популяции: 1) подразделенность вида на множество свободно скрещивающихся внутри себя субпопуляций генетически эффективного объема N, каждая из которых с равной вероятностью и с одинаковой интенсивностью m обменивается генами с любой другой; 2) большая панмиктическая популяция («материк»), окруженная множеством изолированных, генетически дифференцированных малых колоний («острова»), каждая из которых получает гены с «материка» с интенсивностью m на поколение. Эффектами обратной миграции можно пренебречь.

Мерой случайной дифференциации субпопуляций в такой системе служит межгрупповая варианса генных частот:

,

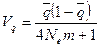и, следовательно, условие равновесия между дрейфом и миграцией генов в терминах F_ST – статистики может быть записано как:

.

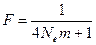Более строгое решение относительно V_q задается формулой (Wright, 1943):

.

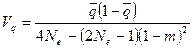Как следствие взаимодействия дрейфа и миграции мы имеем вероятностное распределение частот генов. В любой момент времени T оно представляет функцию от 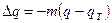как меры систематического давления миграции и 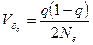– выборочной вариансы частоты гена в одном поколении за счет изоляции, т. е. случайного дрейфа (Wright, 1938):

.

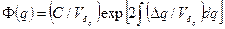Если мы обозначим через q_i частоту гена в i-й группе 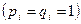, а через q – частоту этого же гена в подразделенной популяции как в целом, то характерные для нее средняя частота гена и ее варианса будут:

, .

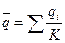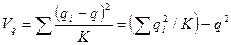Соответственно частоты зигот (генотипов) равны

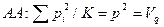
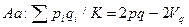
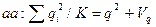
Сопоставляя частоты генотипов с их частотами в популяции, характеризующейся коэффициентом инбридинга F, получим соотношение

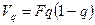или .

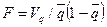Поскольку величина F характеризует подразделенную популяцию в целом, то соответствующие частоты генотипов в ней равны частотам, которые были бы свойственны отдельной инбредной популяции. Иными словами, «подразделенность популяции на отдельные скрещивающиеся группы формально эквивалентна наличию инбридинга во всей популяции» [Ли, 1978].

Общая формула стационарного распределения частот генов в островной модели представляет b-функцию плотности вероятности следующего вида:

,

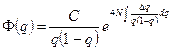где С – нормирующий множитель, подбираемый так, чтобы

, .

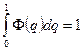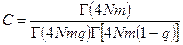В зависимости от того, каким сочетанием случайных и систематических факторов задается распределение, оно принимает вид:

а) при уравновешивании случайного дрейфа генов их миграцией

,

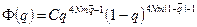где p и q– частоты аллелей в субпопуляциях; 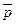и 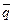– средние частоты аллелей для подразделенной популяции как целого; N – эффективный размер популяции; m – коэффициент миграции;

б) при объединенном эффекте воздействия изоляции, миграции и отбора:

,

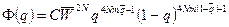где все обозначения те же, что и в предыдущем выражении, а 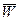– средняя внутрилокусная приспособленность популяции, определяемая через суммирование приспособленностей генотипов с учетом их частот.

Стационарные распределения могут описывать: 1) распределения частот аллелей многих локусов в одной и той же популяции в случае нейтральности или при примерно одинаковом давлении отбора на каждый локус; 2) распределение генных частот какого-либо локуса в последовательных поколениях одной и той же стационарной популяции; 3) распределение частот аллелей одного или нескольких локусов в совокупности полностью или частично изолированных популяций. Все три типа распределений математически эквиваленты.

В островной модели величина коэффициента миграции генов не зависит от степени удаленности популяций. Райт [Wright, 1943] и Малеко [1955, 1957] математически исследовали ту же популяцию, в которой интенсивность обмена между субпопуляциями зависит от расстояния. Эта модель носит название «изоляция расстоянием» и предполагает популяцию, непрерывно распределенную на большой территории, существенно превышающей радиус индивидуальной активности особи в репродуктивный период. Особенности локальной дифференциации в такой системе зависят от репродуктивной величины, или «соседства», откуда случайно происходят родители, а также от размерности ареала.

Согласно С. Райту [1951], размер соседства приблизительно соответствует числу генетически эффективных особей внутри круга, радиус которого равен удвоенному стандартному отклонению s протяженности миграции в одном направлении в данном поколении (или – что то же – дистанции между местами рождения родителей и потомков).

Дифференциация очень велика, когда 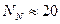, намного меньше, но все же достаточно выражена при 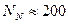и почти соответствует панмиксии, когда .

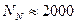М. Кимура [1953] предложил другую популяционную модель популяционной структуры. Она носит название «лестничная модель» и представляет ситуацию, промежуточную между райтовской островной моделью и моделями непрерывно распределенных популяций Райта и Малеко.

Лестничная структура миграции генов. В этой модели, как и в островной, рассматривается совокупность колоний, однако обмен особями происходит только между соседними колониями, и, таким образом, непосредственно зависит от удаленности колоний друг от друга.

При равновесии межпопуляционная варианса генных частот

,

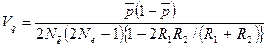где 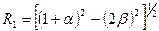; 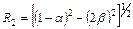, в которых 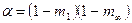и 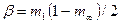; в этих уравнениях m₁ – интенсивность миграций между смежными колониями, а 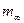– давление миграции генов извне на всю совокупность колоний (соответствует коэффициенту m в островной модели С. Райта). Когда m₁= 0, то 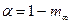, , 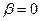и выражение сводится к формуле С. Райта. Островная модель С. Райта, таким образом, представляет собой частный случай лестничной модели в отсутствие обмена генами между соседними колониями.

Важнейшая особенность подразделенности, также исследованная теоретически, – способность подразделенных популяций поддерживать значительно большее генетическое разнообразие в сравнении с панмиктическими популяциями сопоставимого размера. Считается, что именно такое разнообразие и позволяет подразделенной популяции более эффективно реагировать на изменения среды и вслед за ними изменять свою генотипическую структуру – тезис, играющий решающую роль в эволюционной концепции С. Райта, известной под названием «теория смещающегося равновесия», в которой «поверхность» 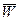изображается топографической картой с вершинами и долинами на едином ландшафте генных комбинаций. В этой модели важнейшее заключение состоит в том, что «эволюционный процесс зависит от постоянно смещающегося баланса между факторами стабильности и изменений и что наиболее благоприятное условие для этого – наличие тонко подразделенной структуры, в которой изоляция и перекрестная коммуникация поддерживаются в соответствующем равновесии» [Wright, 1951].