Формирование признакого пространства методом ортогонализации

Следующая систематическая процедура способна итеративно выделять наиболее значимые признаки, являющиеся линейными комбинациями входных переменных: (подмножество входов является частным случаем линейной комбинации, т.е. формально можно найти лучшее решение, чем то, что доступно путем отбора наиболее значимых комбинаций входов).

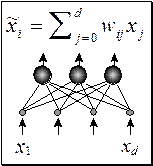
Рисунок 51. Выбор наиболее значимых линейных комбинаций входных переменных.

Для определения значимости каждой входной компоненты будем использовать каждый раз индивидуальную значимость этого входа:.

Подсчитав индивидуальную значимость входов, находим направление в исходном входном пространстве, отвечающее наибольшей (нелинейной) чувствительности выходов к изменению входов. Это градиентное направление определит первый вектор весов, дающий первую компоненту пространства признаков:

.

Следующую компоненту будем искать аналогично первой, но уже в пространстве перпендикулярном выбранному направлению, для чего спроектируем все входные вектора в это пространство:

.

В этом пространстве можно опять подсчитать “градиент” предсказуемости, определив индивидуальную значимость спроектированных входов, и так далее. На каждом следующем этапе подсчитывается индивидуальная значимость для проекции входов

,

что не требует повышения размерности box-counting анализа. Таким образом, описанная выше процедура позволяет формировать пространство признаков произвольной размерности - без потери точности.

Заключение

Конечно, описанными выше методиками не исчерпывается все разнообразие подходов к ключевой для нейро-анализа проблеме формирования пространства признаков. Мы не упомянули, в частности, генетические алгоритмы, которые в совокупностью с методикой box-counting являются весьма перспективным инструментом. Ничего не было сказано также о методике разделения независимых компонент (blind signal separation), расширяющей анализ главных компонент. Необъятного не объять. Главное, чтобы за деталями не затерялся основополагающий принцип предобработки данных: снижение существующей избыточности всеми возможными способами. Это повышает информативность примеров и, тем самым, качество нейропредсказаний.

Bishop C.M. (1995) Neural Networks and Pattern Recognition. Oxford Press.

Voss R.F. (1986) “Random Fractals, Characterization and Measurement”, in Scaling Phenomena in Disordered Systems, R.Pynn and A.Skjeltorp, Eds., Plenum, NewYork.

Keller J.M., Chen S., and Crownover R.M. (1988) “Texture Description and Segmentation through Fractal Geometry”. Computer Vision, Graphics, and Image Processing, 45, 150-166.

Pineda F.J., and Sommerer J.C. (1994) “Estimating Generalized Dimensions and Choosing Time Delays: A Fast Algorithm”, in Time Series Prediction, A.S.Weigend, N.A.Gershenfeld, Eds., Addison-Wesley, p.367-385.

Rissanen J. (1990) “Complexity of Models”, in Complexity, Entropy and the Physics of Information, Ed. W.H.Zurek; Addison-Wesley, Redwood City, California, p. 117-125.

Предсказание финансовых временных рядов

Что обеспечивает доходность бизнеса, основанного на предсказаниях? Какова методика предсказания временных рядов? Специфика финансовых временных рядов. Как подбирать признаковое пространство? Какой функционал ошибки лучше? Норма прибыли нейросетевой игры на реальных данных.

& И будущаго, конечно, не знаютъ ни Ангелы Божiи, ни демоны; однако, они предсказываютъ.
Св. Иоанн Дамаскин, Точное изложение православной веры