ПОНЯТИЕ ОБ ИЗМЕРЕНИИ
Измерением называется сравнение измеряемой величины 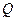 с другой величиной
с другой величиной 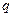 аналогичной физической природы, принятой за единицу. Формула измерения:
аналогичной физической природы, принятой за единицу. Формула измерения:
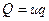 (1.1)
(1.1)
где 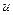 – числовое значение. Пример: Глубина скважины (
– числовое значение. Пример: Глубина скважины ( 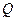 ) равна 2015 (
) равна 2015 ( 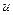 ) метров (
) метров ( 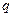 ).
).
Выделяют четыре вида измерений, из которых важнейшими являются два: прямые измерения и косвенные измерения.
Прямыми называются измерения, результат которых находят с помощью прямого сравнения измеряемой величины с единицей, либо с помощью отсчетных устройств измерительных приборов.
Косвенными называются измерения, результат которых находят с помощью формул – в виде математической зависимости от аргументов, полученных прямыми измерениями:
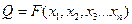 , 1.2)
, 1.2)
где символ 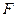 означает некоторую функцию от аргументов
означает некоторую функцию от аргументов 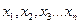 . Например, можно измерить косвенным способом крутящий момент на вращателе буровой установки, пользуясь формулой
. Например, можно измерить косвенным способом крутящий момент на вращателе буровой установки, пользуясь формулой
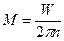 ,
,
где 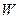 – мощность по показаниям ваттметра, а
– мощность по показаниям ваттметра, а 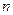 – частота вращения вращателя по показаниям тахометра.
– частота вращения вращателя по показаниям тахометра.
В основе метрологии – науке об измерениях – лежит принцип обеспечения единства измерений. Этот принцип требует одинаковости (в пределах заданной точности) результата измерений той же самой величины, в каких бы условиях эти измерения не производились. Важнейшим условием соблюдения принципа единства измерений является единство единиц измерений.
В прошлом многие страны имели собственные единицы измерений, свои единицы также имели отдельные отрасли индустрии и науки. Это сильно затрудняло использование результатов, полученных в одних странах (или отраслях промышленности и науки), другими странами (отраслями). Для ликвидации этих барьеров в 1960 г была создана международная система единиц СИ (System International), которая была рекомендованы для использования всеми государствами – членами Организации Объединенных Наций – и к настоящему времени принята большинством развитых стран.
Любая система единиц состоит из двух групп единиц: основных единиц и производных единиц. Основные единицы принимаются произвольно или из соображений удобства. Система СИ включает семь основных единиц: длины – метр (м); времени –секунда(с); массы –килограмм(кг); силы тока–Ампер(А);температуры –Кельвин( 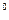 К); силы света –кандела(Кд);количества вещества – моль. Кроме того имеется две дополнительные единицы: единица плоского угла – радиан(рад)и единица телесного угла – стерадиан. Основные единицы соответствуют разделам физики. Так, три первых единицы соответствуют “механике”; четвертая – “электричеству”; пятая – “теплоте”; шестая – “свету“; седьмая – “атомной физике”.
К); силы света –кандела(Кд);количества вещества – моль. Кроме того имеется две дополнительные единицы: единица плоского угла – радиан(рад)и единица телесного угла – стерадиан. Основные единицы соответствуют разделам физики. Так, три первых единицы соответствуют “механике”; четвертая – “электричеству”; пятая – “теплоте”; шестая – “свету“; седьмая – “атомной физике”.
Производные единицы выводятся из основных единиц, если известны физические законы, связывающие соответствующие величины (т. е. величины, которые имеют основные единицы и величины, которые имеют производные единицы). Вывод производных единиц осуществляется по формуле размерности:
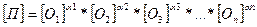 , (1.3)
, (1.3)
где квадратные скобки означают, что это не сами величины ( 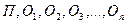 ) а их единицы измерения, а
) а их единицы измерения, а 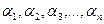 – показатели степени (их называют размерности), характеризующие физические законы, связывающие величины. Для системы СИ формула (1.3) выглядит как:
– показатели степени (их называют размерности), характеризующие физические законы, связывающие величины. Для системы СИ формула (1.3) выглядит как:
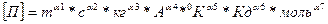 (1.4)
(1.4)
Пример: единица силы : кг*м/с 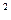 , (получившая название Ньютон (Н)). Эта единица в соответствии с формулой (1.4) может быть представлена как
, (получившая название Ньютон (Н)). Эта единица в соответствии с формулой (1.4) может быть представлена как
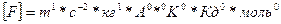
Единица силы получена в соответствии со вторым законом Ньютона
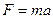 ,
,
где 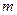 – масса, (единица кг)
– масса, (единица кг) 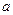 – ускорение (единица м/с
– ускорение (единица м/с 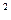 ).
).
Измерения всегда сопровождаются ошибками. Абсолютная ошибка измерения
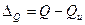 , (1.5)
, (1.5)
где 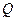 – результат измерения,
– результат измерения, 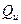 – истинное значение. Однако истинное значение установлено быть не может (ввиду обязательного наличия ошибок), поэтому практически более правильна формула
– истинное значение. Однако истинное значение установлено быть не может (ввиду обязательного наличия ошибок), поэтому практически более правильна формула

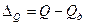 , (1.6)
, (1.6)
где 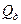 – действительное значение, которое представляет собой результат измерения той же величины, полученной с максимально-возможной в данных условиях точностью. Абсолютная ошибка измерения имеет те же единицы, что и измеряемая величина.
– действительное значение, которое представляет собой результат измерения той же величины, полученной с максимально-возможной в данных условиях точностью. Абсолютная ошибка измерения имеет те же единицы, что и измеряемая величина.
Относительная ошибкаизмерения
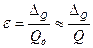 . (1.7)
. (1.7)
Поскольку и числитель и знаменатель имеют одинаковые размерности, относительная ошибка есть величина безразмерная.
Относительная ошибка измерения есть мера точности измерения, которая представляет собой величину, обратную относительной ошибке (чем меньше 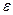 , тем выше точность измерения).
, тем выше точность измерения).
В зависимости от причины, их вызвавшей, ошибки измерений бывают инструментальные, методические и субъективные. Инструментальные ошибки зависят от измерительных средств. Такие ошибки подразделяются на:
– Шкальные (неверное нанесение шкалы ).
– Остаточной деформации в механических передачах и стрелке – если прибор был вынужден измерять величину, превышающую его верхний предел.
– Трения (в механических деталях прибора). При измерении возрастающей величины ошибки трения занижают эту величину, а при измерении уменьшающейся величины – завышают. (см. ниже формулы (5.15) – (5.17)).
– Старения (в процессе эксплуатации пружины теряют свою жесткость).
– Ошибки, вызванные люфтами. Если между зубьями шестерен имеется люфт (зазор), то при смене направления вращения ведомая шестерня начинает вращаться лишь после того, как ведущая, выбирая люфт, уже повернулась на некоторый угол. Этот угол и будет причиной ошибки. Люфты возрастают с течением времени от износа деталей.
Методические ошибки зависят не от самого прибора, а от методики его использования. Сюда относятся такие факторы, как: а) место расположения прибора;
б) правильность выбора прибора данного принципа действия для производства данных конкретных измерений; в) учет всех факторов, могущих оказать влияние на показания.
Рассмотрим методические погрешности на примере измерения расхода промывочной жидкости.
а) Место расположения бурового расходомера. Для эффективного удаления шлама с забоя скважины к долоту необходимо подавать определенный расход жидкости. Оценка этого расхода, как правило, производится по показаниям расходомера, установленного в нагнетательной линии сразу после бурового насоса. Однако далее промывочная жидкость движется к долоту через бурильную колонну, и часть ее может просачиваться сквозь соединения бурильных труб в кольцевое пространство и по нему возвращаться к устью скважины, минуя долото. Из-за утечек истинный расход, подаваемый к долоту, будет на определенную величину (методическую ошибку) меньше, показываемого расходомером. Эту ошибку можно устранить установкой расходомера прямо над долотом (что представляет собой сложную задачу).
б) Соответствие принципа работы расходомера свойствам измеряемой жидкости. Если попытаться использовать электромагнитный расходомер (см. ниже – рис. 8.5) для измерения расхода нефти, то он не будет давать показаний. Дело в том, что электромагнитный расходомер может работать только на токопроводящих жидкостях. В описанном случае необходимо использовать расходомер другого типа (например, расходомер с переменным перепадом давления – рис. 8.1).
в) Расходомер должен работать на той жидкости, которая была использована при его градуировке (нанесении шкалы). Обычно градуировка производится на воде. Если же расходомер будет после этого использоваться, например, на глинистом растворе, то возникнет значительная методическая ошибка, вызванная тем фактом, что плотность глинистого раствора больше плотности воды. Ошибка устраняется использованием таблиц поправок на фактическую плотность.
Субъективные ошибки зависят от наблюдателя, его квалификации и физического состояния. Например, типичной субъективной ошибкой является ошибка параллакса, вызванная неправильным положением глаза. Глаз должен находиться в плоскости, перпендикулярной циферблату и расположенной вдоль оси стрелки. Если глаз будет находиться левее этой плоскости, то оценка будет завышенной, правее – заниженной.
В зависимости от характера, который принимают ошибки при повторных измерениях, ошибки бывают случайными, систематическими и так называемыми “промахами”. Случайные ошибки при повторных измерениях случайным образом изменяются по величине и знаку (таблица 1.1 – серия измерений номер 1)
Таблица 1.1 – Ошибки при повторных замерах давления, равного 1.5 МПа
| Серия измере-ний | 1 (случайные – первый рабочий манометр) | Результат | 1.49 | 1.47 | 1.51 | 1.48 | 1.53 |
| Ошибка | -0.01 | -0.03 | 0.01 | -0.02 | 0.03 | ||
| 2 (систематические – в торой рабочий манометр) | Результат | 1.58 | 1.58 | 1.58 | 1.58 | 1.58 | |
| Ошибка | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 |
Случайные ошибки бывают вызваны суммарным влиянием нескольких одновременно действующих причин (сотрясения, движения воздуха, наличие в нем пыли, колебания питающего напряжения и частоты – если прибор электрический)
Есть два основных способа борьбы со случайными ошибками: стабилизация внешних условий и выведение среднего значения. В таблице 1 среднее значение по пяти замерам составило 1.496, т.е. его ошибка равна всего -0.004 (по абсолютной величине в 2.5 раза меньше самой малой ошибки отдельного частного значения).
Систематические ошибки при повторных измерениях либо остаются неизменными, либо изменяются по определенному закону (последнее относится к часам, которые, например, “бегут” на 2 минуты в сутки). При этом систематическая ошибка имеет, как правило, только одну причину.
Есть два основных способа борьбы с систематическими ошибками: внесение поправки и корректировка работы прибора (юстирование). Чтобы в результат измерения внести поправку, необходимо прибавить к нему систематическую ошибку с обратным знаком. Так, в серии измерений номер 2 таблицы 1.1 имеется: систематическая ошибка, равная 0.08 МПа. Внеся поправку, получим: 1.58 – 0.08 = 1.5 МПа
Второй способ может заключаться в том, что если систематическая ошибка является, например, следствием неверного нанесения шкалы, то эту ошибку можно исправить, переписав шкалу (путем повторного проведения градуировки).
Реально-проводимые измерения обычно включают как случайные, так и систематические ошибки, однако следует указать, что чем грубее измерительные средства и сложнее условия их функционирования, тем выше роль систематических ошибок. Это, в частности, относится к измерениям, проводимым на буровых работах
Промахом называется резко выделяющееся из ряда значение ошибки измерений, вызванное какими-либо чрезвычайными обстоятельствами как объективного, так и субъективного характера. Пример – резкое отклонение показаний электрического прибора от ожидаемых значений в результате кратковременного скачка частоты питающего напряжения.
Косвенные измерения (формула 1.2) представляют собой результат математической обработки результатов прямых измерений. Поэтому, если в последних наличествуют ошибки, то они есть и в полученных на их основе результатах косвенных измерений.
Абсолютная ошибка косвенного измерения определяется по формуле:
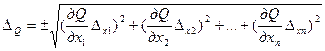 . (1.8)
. (1.8)
Таким образом функцию (1.2) надо последовательно продифференцировать по каждому аргументу (взять частные производные). После этого вычисляют числовые значения полученных величин, подставляют значения ошибок аргументов и находят 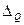 .
.
Пример: Необходимо вычислить массу одного метра бурильной трубы по выражению
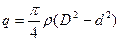 , (1.9)
, (1.9)
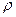 – плотность материала бурильных труб,
– плотность материала бурильных труб, 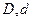 – наружный и внутренний диаметры трубы.
– наружный и внутренний диаметры трубы.
По результатам прямых измерений получено: 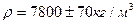 ;
; 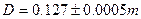 ,
, 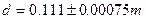 (после знака
(после знака 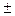 приведены ошибки, с которыми измерены соответствующие параметры, т. е.
приведены ошибки, с которыми измерены соответствующие параметры, т. е. 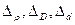 соответственно).
соответственно).
Проведя дифференцирование получаем:
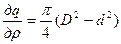 ;
; 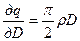 ;
; 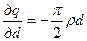 .
.
Подставив в выражения производных известные значения параметров, помножив на соответствующие ошибки и возведя результаты в квадрат, получим слагаемые под корнем выражения 1.8. Произведя суммирование и извлечение корня, получим искомую абсолютную ошибку косвенного измерения массы одного метра трубы: 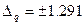 кг/м .
кг/м .
Сама эта масса согласно формуле (1.9) равна: 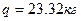 /м. По формуле (1.7) находим относительную ошибку:
/м. По формуле (1.7) находим относительную ошибку: 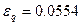 .
.
Рекомендуемая литература: 1. с. 34 – 54, 73 – 77
Контрольные вопросы
1. Что называется измерением?
2. Какие бывают виды измерений?
3. Что такое система единиц измерений?
4. Что такое ошибки измерений, разновидности ошибок?
5. Как вычисляют ошибки косвенных измерений?
Дата добавления: 2015-06-27; просмотров: 2041;
