В Z-единицах
| Показатели | Оценочные категории | ||||
| Z(k)обн | - | 1,64 | 1,04 | 0,39 | -0,39 |
| Z(k)лт | - | 0,28 | -0,52 | -1,13 | -2,05 |
Рабочая характеристика, соответствующая данным табл.13, изображена на рис.16 и представляет собой отрезок прямой, проходящий через четыре точки. Определение параметров линейной функции, аппроксимирующей экспериментальные данные, осуществляется по методу наименьших квадратов, описание которого можно найти в любом руководстве по математической статистике.
Поскольку в методе оценки получается несколько пар (точнее – (k – 1) пара) значений Z(k)обн и Z(k)лт (в рассматриваемом примере четыре), то может быть рассчитано и столько же значений показателя чувствительности d¢. В теории или в идеальном эксперименте все эти значения d¢ должны совпасть. Однако в реальном эксперименте этого не происходит. Поэтому в качестве итогового показателя чувствительности может быть взято среднее арифметическое значение всех полученных значений d¢, каждое из которых рассчитывается согласно формуле (23):
= 
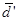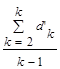. (26)
В примере, согласно данным табл.13, имеем: d¢2 = 1,36; d¢3 = 1,56; d¢4 = 1,52; d¢5 = 1,66, и, соответственно:
= 
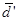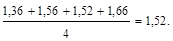
Обращает на себя внимание еще один возможный показатель, который может быть получен в методе оценки – ширина диапазона изменений порогов принятия решения λ0 , возникновение которого обусловлено использованием нескольких оценочных категорий. Это уже характеристика механизмов принятия решения, отражающих психологические особенности личности испытуемого. Косвенно величина этого показателя ( Δλ0 ) может быть оценена через разброс значений Zобн и Zлт для крайних из использованных значений оценочных категорий k.
 |
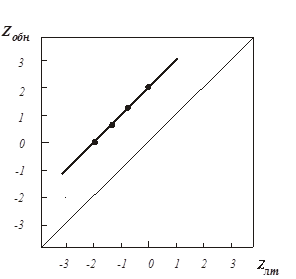Теоретически такой разброс значений должен быть одинаков для Zобн и Zлт – графически (см. рис.16) величина разброса представляет собой расстояние между крайними точками РХ, взятое либо по оси Zобн, либо по оси Zлт. Однако на практике такое равенство встречается редко и является исключением.
Рис.16. РХ, построенная по данным метода оценки
Поэтому можно использовать процедуру приближенного вычисления величины разброса D(λ0), представляющую собой косвенную оценку величины Δλ0:
D(λ0) = [(Z(2)обн – Z(k)обн)+ (Z(2)лт – Z(k)лт)] ∕ 2. (27)
Так, для данных нашего примера:
D(λ0) = [(1,64 – (-0,39))+ (0,28 – (-2,05))] ∕ 2 = 2,18
Значение величины D(λ0), меняющееся в пределах от нуля до шести, позволяет оценить пластичность испытуемого, его способность изменять критерии, используемые при выполнении задания. В определенной степени это значение отражает и готовность испытуемого к применению более рискованной («смелой») стратегии оценивания.
Дата добавления: 2015-03-09; просмотров: 642;