Основные определения. В разд. 5.2 рассматривался расчет жестких стержней, подверженных внецентренному растяжению-сжатию

В разд. 5.2 рассматривался расчет жестких стержней, подверженных внецентренному растяжению-сжатию. Расчет этих стержней велся по недеформированному состоянию, т. е. при определении внутренних усилий не учитывалось искривление оси стержня. Для гибких стержней необходимо учитывать влияние деформаций изгиба на внутренние усилия. Такой расчет носит название расчета по деформированному состоянию.

При расчете по деформированному состоянию изгибающий момент вызывается не только поперечной нагрузкой, но и сжимающей силой. Будем рассматривать стержень, подверженный действию поперечной, примерно симметричной относительно середины пролета нагрузки, действующей в плоскости симметрии поперечного сечения, и сжимающей силы F. В этом случае наибольший прогиб имеет место по середине пролета. Максимальное нормальное напряжение в опасном сечении стержня определяется по формуле

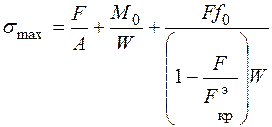, (6.10)

где 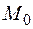– изгибающий момент в опасном сечении, вызванный действием только поперечной нагрузки (при отсутствии сжимающей силы); 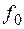– прогиб по середине пролета, вызванный только поперечной нагрузкой; 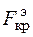– значение критической нагрузки, вычисляемой по формуле Эйлера при изгибе стержня в плоскости действия поперечной нагрузки; 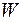– момент сопротивления сечения стержня относительно той оси, которая будет нейтральной при изгибе от поперечной нагрузки.

В формуле (6.10) два первых слагаемых определяют наибольшее напряжение в стержне при расчете по недеформированному состоянию, третье слагаемое показывает вклад сжимающей силы в напряжения от изгиба. Видно, что зависимость напряжения от сжимающей нагрузки нелинейная, поэтому проверку прочности стержня нельзя производить расчетом по допускаемым напряжениям. Проверку прочности гибких сжато-изогнутых стержней необходимо вести расчетом по предельному состоянию, обеспечивая запас прочности не по напряжениям, а по нагрузке. В этом случае условие прочности имеет вид

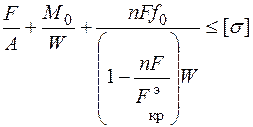, (6.11)

где n – нормируемый коэффициент запаса прочности материала.

Проверка жесткости гибкого сжато-изогнутого стержня расчетом по деформированному состоянию производится по формуле

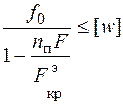. (6.12)

В формуле (6.12) 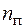– коэффициент запаса по прогибам, обычно принимаемый равным коэффициенту запаса прочности .

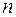Кроме проверки прочности и жесткости по условиям (6.11), (6.12), необходимо проверить условие устойчивости (6.6) гибкого стержня и обеспечить невозможность потери устойчивости стержня в плоскости наименьшей жесткости, обычно перпендикулярной плоскости действия поперечной нагрузки.