Триангуляционная модель поверхностей

Триангуляционная модель данных (нерегулярная триангуляционная сеть, TIN) предназначена для описания поверхностей. В качестве моделируемой поверхности может выступать рельеф земной поверхности (рис.15) или распределение какого-то параметра по земной поверхности, например, загрязнения окружающей среды, количества выпадающих осадков или среднегодовой температуры.

Заметим, что для моделирования поверхностей может использоваться и растровая модель, когда в каждом пикселе растра задается высота моделируемой поверхности. Однако триангуляционная модель имеет ряд преимуществ по сравнению с растровой. В первую очередь, это более высокая точность моделирования и обычно меньшие затраты памяти. Во-вторых, в триангуляционной модели можно в явном виде представлять резкие изломы поверхности, т.е. точки и линии, вдоль которых резко меняется кривизна поверхности (вершины гор, границы оврагов, обрывы рек, границы искусственных сооружений). В растровой модели предполагается, что вся моделируемая поверхность является гладкой поверхностью.

Исходными данными для построения триангуляционной модели поверхности служат высотные отметки, изолинии, а также различные структурные линии, меняющие форму поверхности. В основе триангуляционной модели данных лежит триангуляция – особая структура данных из вычислительной геометрии, определенная на плоскости. В самом общем понимании триангуляция – это пленарный граф, построенный на множестве заданных узлов и разбивающий всю плоскость на треугольники и одну внешнюю бесконечную фигуру.

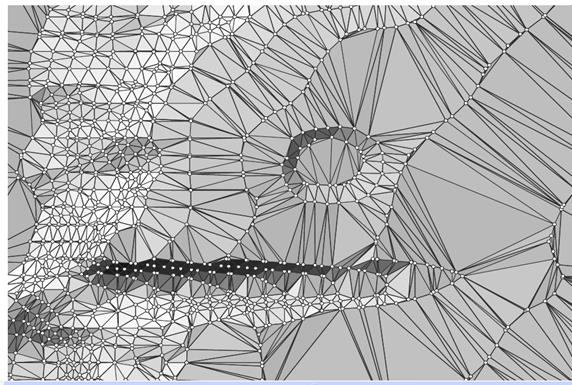
Рис. 15. Триангуляционная модель поверхности земли

Триангуляционная модель данных содержит 3 основных типа данных: узлы, ребра и треугольники (рис. 16).

Узлы в триангуляции характеризуются координатами (х,у,г). Ребра в триангуляции являются отрезками, соединяющими два некоторых узла. Большинство рёбер в триангуляции в явном виде не представляются, т.к. их можно всегда косвенно получить через треугольники. В явном виде представляются только особые ребра, для которых нужно хранить дополнительную информацию, например, признак структурности линии или то, что поверхность не сохраняет гладкость вдоль этой линии (рис.15).

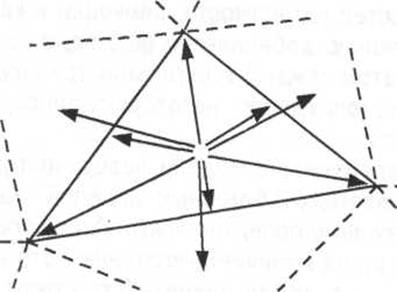
Рис.16. Связи объектов в

триангуляционной модели данных

Контрольные вопросы

1. Дать определение пространственного объекта.

2. Перечислить базовые типы пространственных объектов.

3. Что такое векторные объекты? В каких моделях они используются?

4. Что такое модель данных?

5. Привести примеры векторных моделей.

6. Что называют слоем карты?

7. Дать определение цифровой модели местности и цифровой модели рельефа.

8. Какие модели данных допустимы в шейп-моделях?

9. Для чего предназначена модель транспортной сети?

10. Что такое растровая модель данных?

11. Что подразумевается под процедурами векторизации и растеризации?

12. Для чего предназначена триангуляционная модель данных?