Эффективное кодирование
Этот вид кодирования используется для уменьшения объемов информации на носителе - сигнале.
Для кодирования символов исходного алфавита используют двоичные коды переменной длины: чем больше частота символа, тем короче его код. Эффективность кодаопределяется средним числом двоичных разрядов для кодирования одного символа – lср по формуле
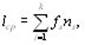
где k – число символов исходного алфавита;
ns – число двоичных разрядов для кодирования символа s;
fs – частота символа s; причем
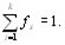
При эффективном кодировании существует предел сжатия, ниже которого не «спускается» ни один метод эффективного кодирования - иначе будет потеряна информация. Этот параметр определяется предельным значением двоичных разрядоввозможного эффективного кода – lпр:
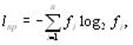
где n – мощность кодируемого алфавита,
fi – частота i-го символа кодируемого алфавита.
Существуют два классических метода эффективного кодирования: метод Шеннона-Фано и метод Хаффмена. Входными данными для обоих методов является заданное множество исходных символов для кодирования с их частотами; результат - эффективные коды.
Метод Шеннона-Фано
Этот метод требует упорядочения исходного множества символов по не возрастанию их частот. Затем выполняются следующие шаги:
а) список символов делится на две части (назовем их первой и второй частями) так, чтобы суммы частот обеих частей (назовем их Σ1 и Σ2) были точно или примерно равны. В случае, когда точного равенства достичь не удается, разница между суммами должна быть минимальна;
б) кодовым комбинациям первой части дописывается 1, кодовым комбинациям второй части дописывается 0;
в) анализируют первую часть: если она содержит только один символ, работа с ней заканчивается, – считается, что код для ее символов построен, и выполняется переход к шагу г) для построения кода второй части. Если символов больше одного, переходят к шагу а) и процедура повторяется с первой частью как с самостоятельным упорядоченным списком;
г) анализируют вторую часть: если она содержит только один символ, работа с ней заканчивается и выполняется обращение к оставшемуся списку (шаг д). Если символов больше одного, переходят к шагу а) и процедура повторяется со второй частью как с самостоятельным списком;
д) анализируется оставшийся список: если он пуст – код построен, работа заканчивается. Если нет, – выполняется шаг а).
Пример 1. Даны символы a, b, c, d с частотами fa = 0,5; fb = 0,25; fc = 0,125; fd = 0,125. Построить эффективный код методом Шеннона-Фано.
Сведем исходные данные в таблицу, упорядочив их по невозрастанию частот:
| Исходные символы | Частоты символов |
| a | 0,5 |
| b | 0,25 |
| c | 0,125 |
| d | 0,125 |
Первая линия деления проходит под символом a: соответствующие суммы Σ1 и Σ2 равны между собой и равны 0,5. Тогда формируемым кодовым комбинациям дописывается 1 для верхней (первой) части и 0 для нижней (второй) части. Поскольку это первый шаг формирования кода, двоичные цифры не дописываются, а только начинают формировать код:
| Исходные символы | Частоты символов | Формируемый код |
| a | 0,5 | |
| b | 0,25 | |
| c | 0,125 | |
| d | 0,125 |
В силу того, что верхняя часть списка содержит только один элемент (символ а), работа с ней заканчивается, а эффективный код для этого символа считается сформированным (в таблице, приведенной выше, эта часть списка частот символов выделена заливкой).
Второе деление выполняется под символом b: суммы частот Σ1 и Σ2 вновь равны между собой и равны 0,25. Тогда кодовой комбинации символов верхней части дописывается 1, а нижней части – 0. Таким образом, к полученным на первом шаге фрагментам кода, равным 0, добавляются новые символы:
| Исходные символы | Частоты символов | Формируемый код |
| a | 0,5 | |
| b | 0,25 | |
| c | 0,125 | |
| d | 0,125 |
Поскольку верхняя часть нового списка содержит только один символ (b), формирование кода для него закончено (соответствующая строка таблицы вновь выделена заливкой).
Третье деление проходит между символами c и d: к кодовой комбинации символа c приписывается 1, коду символа d приписывается 0:
| Исходные символы | Частоты символов | Формируемый код |
| a | 0,5 | |
| b | 0,25 | |
| c | 0,125 | |
| d | 0,125 |
Поскольку обе оставшиеся половины исходного списка содержат по одному элементу, работа со списком в целом заканчивается.
Таким образом, получили коды:
a - 1,
b - 01,
c - 001,
d - 000.
Определим эффективность построенного кода по формуле:
lср = 0,5*1 + 0,25*01 + 0,125*3 + 0,125*3 = 1,75.
Поскольку при кодировании четырех символов кодом постоянной длины требуется два двоичных разряда, сэкономлено 0,25 двоичного разряда в среднем на один символ.
Метод Хаффмена
Этот метод имеет два преимущества по сравнению с методом Шеннона-Фано: он устраняет неоднозначность кодирования, возникающую из-за примерного равенства сумм частот при разделении списка на две части (линия деления проводится неоднозначно), и имеет, в общем случае, большую эффективность кода.
Исходное множество символов упорядочивается по не возрастанию частоты и выполняются следующие шаги:
1) объединение частот:
· две последние частоты списка складываются, а соответствующие символы исключаются из списка;
· оставшийся после исключения символов список пополняется суммой частот и вновь упорядочивается;
· предыдущие шаги повторяются до тех пор, пока ни получится единица в результате суммирования и список ни уменьшится до одного символа;
2) построение кодового дерева:
· строится двоичное кодовое дерево: корнем его является вершина, полученная в результате объединения частот, равная 1; листьями – исходные вершины; остальные вершины соответствуют либо суммарным, либо исходным частотам, причем для каждой вершины левая подчиненная вершина соответствует большему слагаемому, а правая – меньшему; ребра дерева связывают вершины-суммы с вершинами-слагаемыми. Структура дерева показывает, как происходило объединение частот;
· ребра дерева кодируются: каждое левое кодируется единицей, каждое правое – нулем;
3) формирование кода: для получения кодов листьев (исходных кодируемых символов) продвигаются от корня к нужной вершине и «собирают» веса проходимых ребер.
Пример 1. Даны символы a, b, c, d с частотами fa = 0,5; fb = 0,25; fc = 0,125; fd= 0,125. Построить эффективный код методом Хаффмена.
1) объединение частот (результат объединения двух последних частот в списке выделен в правом соседнем столбце заливкой):
| Исходные символы | Частоты fs | Этапы объединения | ||
| первый | второй | третий | ||
| a | 0,5 | 0,5 | 0,5 | |
| b | 0,25 | 0,25 | 0,5 | |
| c | 0,125 | 0,25 | ||
| d | 0,125 |
2) построение кодового дерева:
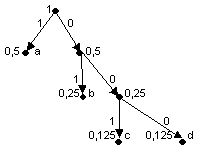
3) формирование кода:
a - 1;
b - 01;
c - 001;
d - 000.
Как видно, полученные коды совпадают с теми, что были сформированы методом Шеннона-Фано, следовательно, они имеют одинаковую эффективность.
Дата добавления: 2015-03-03; просмотров: 1367;
