Плоская прямая ударная волна

Пусть в цилиндре сечением, равным единице, наполненном какой-либо средой, распространяется слева направо плоский скачок давления. Скорость перемещения скачка обозначим D.

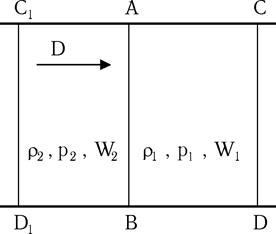
Невозмущенное состояние среды справа от скачка характеризуется величинами r₁, p₁, W₁ ¹ 0. За фронтом скачка имеем параметры r₂, p₂, W₂.

Если учесть собственную скорость частиц в невозмущенной среде W₁, то действительная скорость распространения скачка уплотнения будет D – W₁, а скорость потока за фронтом волны W₂ – W₁.

Рассмотрим скачок уплотнения в системе координат, перемещающейся слева направо со скоростью D. При этом граница AB между возмущенной и невозмущенной зонами останется неподвижной. В этой системе координат невозмущенный поток будет двигаться влево со скоростью D –W₁, а возмущенный со скоростью D –W_­2.

Газ, расположенный между сечениями AB и CD, через одну секунду окажется в объеме между сечениями C₁D₁ и AB.

Из закона сохранения массы:

r₁(D – W₁) = r₂(D – W₂).

Из закона сохранения количества движения (импульс силы равен изменению количества движения):

Ft =M× DW.

При t = 1с и площади сечения также равной 1м² это выражение примет вид:

p₂ – p₁ = r₁(D – W₁)(W₂ – W₁).

Наконец, из закона сохранения энергии:

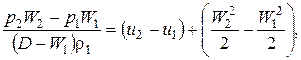
где u_i – удельные внутренние энергии невозмущенного (i = 1) и возмущенного (i = 2) газа;

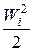– удельные кинетические энергии газа;

p₂W₂ – p₁W₁ – работа, затрачиваемая силами давления на перемещение среды, в единицу времени.

Из этих трех уравнений, введя v_i = 1/r_i, можно путем простых преобразований (*) получить следующие соотношения:

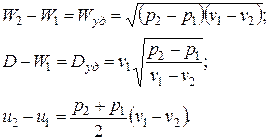
{* Из 2-го уравнения 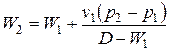. Подставляем в 1-е уравнение ; ;

; ;

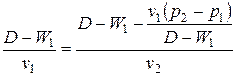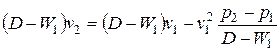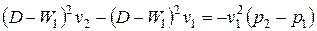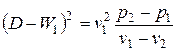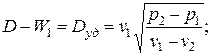
Отсюда 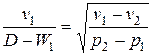. Из 2-го уравнения 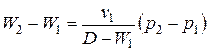. Тогда .

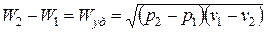Из 3-го уравнения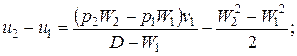

}

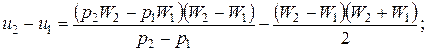
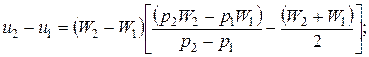
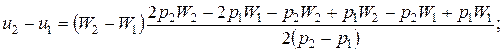
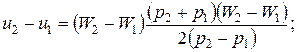
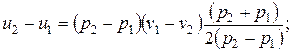
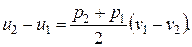Последнее уравнение называется уравнением Гюгонио.

Для идеального газа

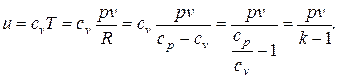
Тогда

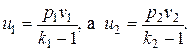
Произведя элементарные преобразования, из уравнения Гюгонио найдем, что

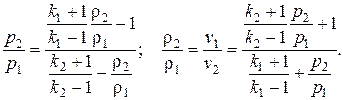
Если волна не слишком сильная, то k₁ = k₂ = k и

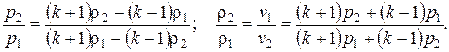
В таком виде эти уравнения носят название ударной адиабаты или адиабаты Гюгонио. Эта адиабата, выражая закон сохранения энергии, является аналогом обычной адиабаты и справедлива для ударных волн в политропных средах.

Таким образом, мы получили систему уравнений:

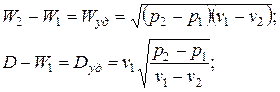
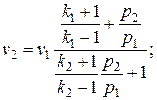(или уравнение Гюгонио в другом виде)

p = f(v,T) – уравнение состояния, например, p₂v₂ = RT₂.

В этой системе уравнений пять неизвестных: p₂, v₂, T₂, W_уд, D_уд, а уравнений – четыре. Следовательно, для того, чтобы вычислить параметры волны, один из них надо задать. Действительно, в одной и той же среде могут наблюдаться ударные волны различной интенсивности, поэтому один из параметров волны надо знать, чтобы вычислить остальные.

Если выразить W₂, p₂ и v₂ как функции скорости звука c₁ невозмущенной среды, полагая W₁ = 0 и W₂ = W и применяя уравнение состояния идеального газа, то получим:

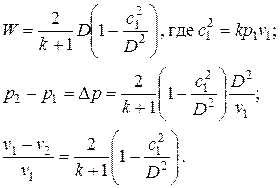
Эти уравнения позволяют получить основные зависимости для звуковых волн. При p₂ ® p₁ и v₂ ® v₁ скорость перемещения скачка D ® c₁ и W ® 0, то есть скорость распространения возмущения равна скорости звука, и перемещения среды не происходит.

Уравнение энергии при W = 0 сводится к du = –p× dv, то есть du + p×dv = 0 (первый закон термодинамики для случая dq = 0, то есть для адиабатного процесса pv^k = const).

Для ударных волн (при p₂ > p₁ и v₂ < v₁) W > 0 и D > 0, причем

то есть D > W.

Таким образом, среда перемещается в направлении распространения фронта ударной волны, но с меньшей, чем фронт, скоростью.

Если наблюдается волна разрежения, то есть p₂ < p₁, то из формулы для Dp видим, что

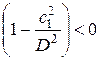, тогда W < 0 и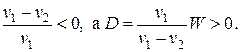

В этом случае среда перемещается в сторону, противоположную направлению распространения волны.

Если термодинамический процесс протекает по адиабате Гюгонио, то энтропия системы возрастает. Из второго закона термодинамики путем несложных преобразований получается:

Если обозначить pv^k = s, то

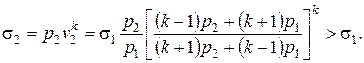
Из данной формулы это явно не просматривается, но легко убедиться в справедливости неравенства, подставив численные значения для k, p₁ и p₂. Причем s₂ > s₁ как при p₂ > p₁, так и при p₂ < p₁.

Так как s₂ > s₁, то s₂ – s₀ > s₁ – s₀, то есть s₂ > s₁. Происходит необратимый процесс.

Дополним полученные соотношения выражением, определяющим температуру на фронте ударной волны для случая идеального газа:

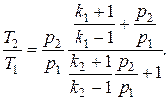
Если k₁ = k₂ = k, то

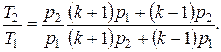
Для сильных ударных волн (p₂ > p₁) полученные нами соотношения можно еще упростить без большой погрешности:

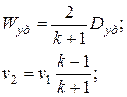
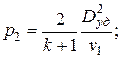
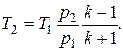
Обратите внимание, что удельный объем (плотность) газа на фронте ударной волны стремится к определенному пределу, зависящему от величины k, то есть в итоге – от температуры на фронте волны.

Вычисления, произведенные Буркхардтом, с учетом диссоциации и ионизации газа в ударной волне показали, что плотность воздуха в ударной волне возрастает примерно в 11 раз при отношении p₂/p₁, лежащем в интервале от 300 до 1500. При меньших или больших значениях этого отношения рост плотности менее значителен.

Таким образом, можно обобщить полученные результаты:

1. Скорость распространения ударных волн всегда больше скорости звука в невозмущенной среде.

2. На фронте ударной волны параметры состояния и движения среды изменяются скачком.

3. Ударные волны сопровождаются перемещением среды в направлении распространения фронта возмущения.

4. Скорость ударной волны зависит от ее интенсивности, что не наблюдается для звуковых волн.

5. При образовании ударных волн энтропия среды возрастает.

6. Ударная волна не имеет периодического характера, а распространяется в виде одиночного скачка уплотнения.

В случае слабых ударных волн можно пользоваться приближенными формулами, полученными из акустической теории ударных волн, то есть при допущении постоянства энтропии в системе или иначе при рассмотрении ударной волны как простой волны сжатия:

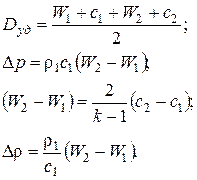
Эти формулы дают приемлемую точность даже для случаев