Условия возникновения ударных волн

Пусть дано некоторое возмущение произвольной амплитуды, бегущее, например, в положительном направлении оси x. Найдем скорость распространения какого-либо заданного состояния среды. Для простых волн все параметры состояния связаны со скоростью перемещения среды W однозначными функциональными зависимостями.

Пусть в некоторый момент времени t₁ в точке x₁ мы имеем скорость среды W = W* и скорость звука c = с*. Определим, в какой точке x₂ будут наблюдаться те же значения W* и c* в некоторый момент времени t₂ > t₁.

Из решения дифференциального уравнения для простой волны получено:

x₁ = (W*+ c*)t₁ + F(W*).

Очевидно, что справедливо должно быть и выражение

x₂ = (W*+ c*)t₂ + F(W*) ,

где F(W*) – произвольная функция.

Из этих выражений найдем величину перемещения заданного состояния среды:

.

Два состояния среды, характеризуемые различными значениями W и c, будут распространяться с постоянными, но различными между собой скоростями. Вследствие этого возмущение будет претерпевать изменения: точки, для которых W и c больше (гребни волн), то есть где плотность среды максимальна, будут перемещаться быстрее, чем другие точки, для которых W + c меньше.

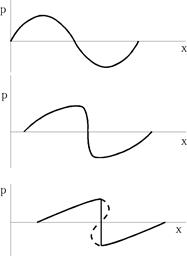
Физически это объясняется тем, что в более плотном газе скорость звука больше, более сжатый газ имеет также большую массовую скорость, направленную в сторону распространения звука.

В результате движения волна будет деформироваться. Области сжатия будут выдвигаться вперед, а области разрежения будут, наоборот, отставать от общего среднего движения газа. Так будет продолжаться, пока фронт волны не станет вертикальным (момент образования ударной волны).

Пересечения фронта, показанного пунктиром, не будет (одна точка x не может иметь одновременно три разных значения плотности). Дело в том, что уравнение, из которого мы получили решение, справедливо лишь до момента возникновения разрывов давления, плотности, температуры. Разрыв означает изменение энтропии, а при решении уравнения предполагалось S = const. Рост энтропии означает рассеивание энергии, то есть обуславливает сильное затухание волны.