Корені, які знаходяться в лівій напівплощині параметру р, дорівнюють для знаменника і для чисельника, а в правій напівплощині відповідно і .

Перехід від якої-небудь точки площини ω до відповідної точки площини р означає поворот радіуса-вектора, проведеного до цієї точки, на 90˚ проти годинникової стрілки, оскільки із відомої формули:

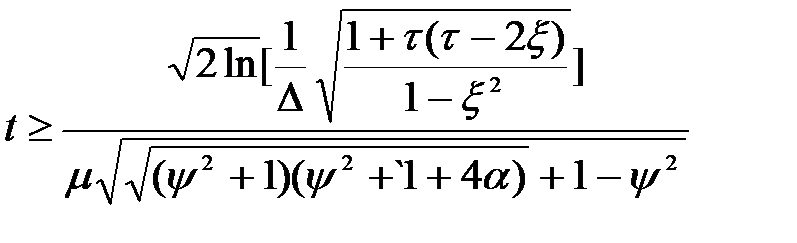. (4.26)

при ωτ=π/2, можна записати, що 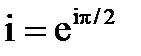, тому .

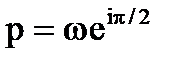Приклад. Розглянемо задачу оптимальної фiльтрацiї, коли на входi випадковий корисний сигнал має перiодичну складову i апроксимований диференцiйною або недиференцiйною функцiями, а перешкода - бiлим шумом. Спектральну щiльнiсть суми корисного сигналу i перешкоди в загальному виглядi представимо так:

,

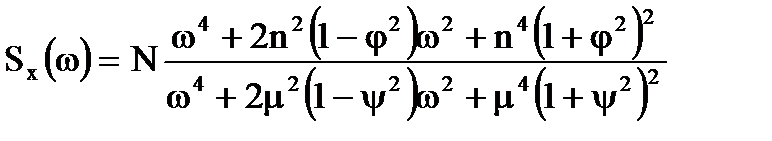де полiноми чисельника i знаменника являють собою добуток чотирьох спiвмножникiв, якi мають дiйсну частину – параметр затухання корисного або сумарного сигналу i уявну частину - резонансну частоту як добуток ступеня регулярностi на параметр затухання корисного i сумарного сигналiв.

Розглянемо спектральну щiльнiсть, апроксимовану диферен цiйною функцiєю. Виконаємо структурний синтез за методикою Ван-Трiса, а для порівняння за методикою виконанням операцiї сепарацiї по теоремi Кошi про лишки (див. додаток 1 приклад 6.1).