Подбор сечений сжатых элементов

Предельное состояние сжатых элементов ферм определяется их устойчивостью, поэтому проверка несущей способности элементов выполняется по формуле

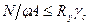(9.5)

где 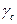- коэффициент условий работы (по прил.14).

Коэффициент “ 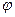”, является функцией гибкости 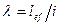и типа сечения (см. прил.8).

Для подбора сечения необходимо наметить тип сечения, задаться гибкостью стержня, определить коэффициент “ 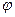” по прил.8 и найти требуемую площадь сечения

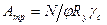(9.6)

При предварительном подборе можно принять для поясов легких ферм 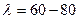, а для решетки 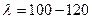. Большие значения гибкости применяются при меньших усилиях.

По требуемой площади подбирается по сортаменту подходящий профиль, определяются его фактические геометрические характеристики А, 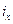, , 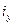находятся 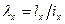; 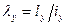. При большей гибкости уточняется коэффициент “ 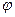” и проводится проверка устойчивости по формуле (9.5). Если гибкость стержня предварительно была задана неправильно и проверка показала перенапряжение или значительное (больше 5-10%) недонапряжение, то проводят корректировку сечения, принимая промежуточное значение между предварительно заданным и фактическим значениями гибкости. Второе приближение, обычно, достигает цели.

Местную устойчивость сжатых элементов можно считать обеспеченной, если толщина полок и стенок профилей больше, чем требуется из условия устойчивости.

Для составных сечений предельные гибкости полок и стенок определяются в соответствии с нормами (см.гл.2).

Пример 9.1.Требуется подобрать сечение верхнего пояса фермы по расчетному усилию

N = 535кН.

Расчетные длины стержня l_x = 2.58; l_y = 5.16м. Материал – сталь С245; R_y = 24кН/см2. Коэффициент условий работы γ_с = 0,95; толщина фасонки 12мм. Поскольку l_y = 2l_x, принимаем тавровое сечение из двух не равнополочных уголков, расположенных узкими полками вместе. Задаемся гибкостью в пределах, рекомендуемых для поясов: λ= 80. Принимаемому сечению соответствует тип кривой устойчивости с и, следовательно, при 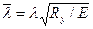= 80 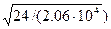= 2,73, φ = 0,611.

Требуемая площадь сечения А_тр = N/(φR_yγ_c) = 535/(0.611 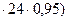= 38.4см2.

Принимаем сечение из двух уголков 125x80x10, поставленных вместе меньшими полками; А = 19,7x2 = 39,4; i_x = 2.26см; i_y = 6,19см (следует обратить внимание, что индексы расчетных осей и осей по сортаменту для не равнополочных уголков могут не совпадать);

λ_x = 258/2.26 = 114; λ_y = 516/6,19 = 83; 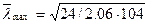= 3,89; φ = 0,417;

N/(φA) = 535/(39.4 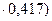= 32.6кН/см2 >R_yφ_c = 22.8кН/см²

Сечение подобрано неудачно и имеет большое перенапряжение. Принимаем гибкость (между предварительно заданной и фактической) λ= 100;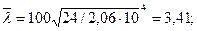

φ= 0,49;

А_тр = 535/(0,49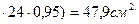

Принимаем два уголка: 160x100x9; А = 22,9 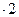= 45,8см²; i_x = 2.85см (i_y не лимитирует сечение); λ_x = 258/2.85 = 90.5;

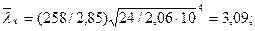φ= 0,546;

N/(φA) = 535/(0.546 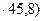= 21.4кН/см² < R_yγ_c = 22.8кН/см²

Оставляем принятое сечение из двух уголков размером 160x100x9.