Основы расчета центрально сжатых стержней

Исчерпание несущей способности длинных гибких стержней, работающих на осевое сжатие, происходит от потери устойчивости (рис.2.4,а).

Поведение стержня под нагрузкой характеризуется графиком (рис.2.4,б), где вначале с ростом нагрузки стержень сохраняет прямолинейную форму, с дальнейшим ростом нагрузки, когда 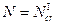стержень теряет свою устойчивость и начинает выпучиваться. Последующий (небольшой) рост внешней нагрузки сопровождается быстрым увеличением поперечного прогиба f. После достижения максимальной нагрузки – второй критической силы 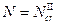- стержень теряет несущую способность (неустойчивое состояние).

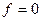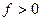Устойчивое состояние может быть при и (точки 1 и 2). Однако при 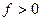стержень может находиться в устойчивом состоянии (точка 2) и

неустойчивом (точка 3) при одинаковой сжимающей силе.

Критическое состояние может быть 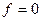при и при 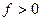(точк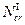и и ).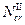

Соответствующее критическое напряжение будет

N_cr¹π²ΕІ π²Εί² π²Ε

Ơ_с_r =-------- = ----- -- = --------- = ------- (2.16)

A l_o²A l_o² λ²

где 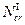- критическая сила равная π²ΕI /l_o² (формула Эйлера); 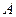- площадь поперечного сечения стержня; заменяя I / A получаем i = 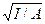- радиус инерции; 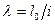- гибкость стержня; 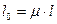- расчетная длина стержня; 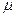- коэффициент приведения, зависящий от способа закрепления концов стержня.

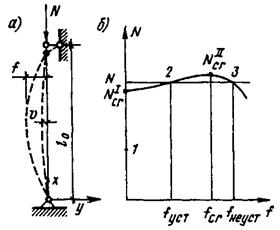Рис.2.4. Работа центрально-сжатого стержня:

а – расчетная схема; б – зависимость между

нагрузкой и прогибом стержня

Формула справедлива при постоянном 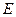, т.е. при напряжениях 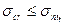, при этом 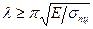. Напряжения 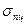- предел пропорциональности.

На практике гибкость центрально сжатых стержней (колонн, элементов ферм, рам и т.д.) составляет примерно половину указанных предельных.

На рис.2.5 показано влияние сечения стержня на критические напряжения. Из приведенных данных видно, что кривые 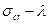для различных сечений и

Разной ориентации осей будут разными. Кривая для двутавра по рис.2.5,а располагается левее, а по рис.2.5,б – правее кривой, соответствующей прямоугольному сечению (рис.2.5,в).

В приведенной классической схеме, в которой предполагается, что в момент потери устойчивости нагрузка остается постоянной, тогда на выпуклой стороне стержня происходит разгрузка и материал начинает работать по упругому

закону. Однако, если деформация сжатия в процессе продольного изгиба растет

или остается постоянной в каждой точке сечения стержня, т.е. разгрузки не происходит, то все сечение находится в пластическом состоянии, характеризуемом касательным модулем деформации .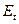

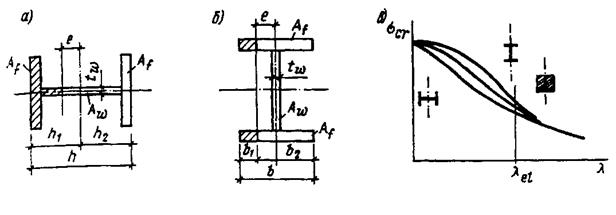Рис.2.5. Влияние формы поперечного сечения стержня на критические напряжения:

а – потеря устойчивости двутаврового стержня в плоскости стенки; б – то же, в

плоскости полок; в – зависимость критических напряжений от гибкости

В этом случае критическое напряжение в пластической области будет

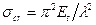(2.17)

В строительных конструкциях встречаются обе схемы работы сжатых стержней. Например, сжатые элементы статически неопределимых систем (ферм, рам) теряют устойчивость по классической схеме - с разгрузкой. В момент потери устойчивости происходит перераспределение усилий между элементами. В колоннах, работающих по статически определимой схеме, будет реализовываться вторая схема – без разгрузки.

До сих пор рассматривался идеально прямой стержень с нагрузкой, приложенной строго по оси. Однако в практике такого не существует. Конструктивное оформление концов сжатых стержней не обеспечивает идеальную центровку, поэтому эти факторы учитываются введением в расчет эквивалентного эксцентриситета сжимающей силы “ 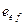”. Он зависит от гибкости и с ростом ее возрастает. В практических расчетах пользуются 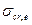, т.е. со случайным эксцентриситетом. Тогда

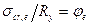, (2.18)

где 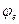- коэффициент устойчивости или его еще называют коэффициентом предельного изгиба при центральном сжатии.

В нормах на проектирование даются формулы и соответствующие таблицы для определения .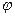

2.7. Основы расчета на прочность стержней, работающих на сжатие или растяжение с изгибом

При одновременном действии на стержень осевой силы 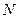и изгибающего момента 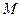(вызванного внецентренным приложением нагрузки 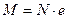) несущая способность его определяется размерами поперечного сечения и предельной прочностью материала.

В упругой стадии работы материала напряжения в поперечном сечении стержня могут быть представлены в виде суммы напряжений от центрального сжатия 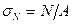и от изгиба .

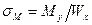2.8. Основы расчета на устойчивость внецентренно сжатых и

сжато - изогнутых стержней

Потеря несущей способности длинных гибких стержней при одновременном действии сжимающей силы и изгибающего момента происходит от потери устойчивости. При этом соответствующее состояние равновесия можно определить так же, как для центрального сжатия, а именно 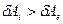- устойчивое состояние; 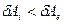- неустойчивое состояние; 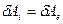- критическое состояние (где 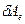и 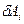- приращение работ внешних и внутренних сил).

Внецентренно сжатые стержни реальных металлических конструкций теряют устойчивость при развитии пластических деформаций.

Критическая сила зависит от эксцентриситета “e”. На практике удобнее пользоваться безразмерным относительным эксцентриситетом m=e/ρ, где ρ=W/A - ядровое расстояние со стороны наиболее сжатой фибры стержня.

Формула проверки устойчивости внецентренно сжатого стержня будет

N / (Aφ_e) 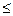R_y γ_c (2.19)

Для обеспечения устойчивости внецентренно сжатых (сжато-изогнутых) стержней целесообразно с целью экономии металла развивать сечение в направлении эксцентриситета. Например, как показано на рис.2.6. При этом возрастает опасность потери устойчивости стержня в перпендикулярном направлении – относительно оси “y” . В связи с этим в формулу проверки устойчивости относительно оси “y” вводится пониженный коэффициент с.

N / cφ_yA 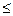γ_cR_y (2.20)

где с =N_cr.M/N_cr =φ_y.M/φ_y; φ_y.N_cr –соответственно коэффициент устойчивости и критическая сила при центральном сжатии; N_cr.M. φ_y.M – критическая сила и соответствующий коэффициент устойчивости центрального сжатия относительно оси “y” при наличии момента в перпендикулярной плоскости. Коэффициент “c” зависит ототносительного эксцентриситета m_x=e/ρ_x.формы поперечного сечения стержня и гибкости λy.

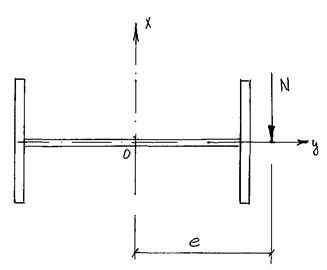Рис.2.6. Наиболее рациональное положение двутаврового сечения при внецентренном сжатии стержней

2.9. Расчет элементов металлических конструкций при воздействии переменных нагрузок (проверка на усталость)

При действии переменных многократно повторяющихся нагрузок разрушение конструкции может произойти от усталости металла при напряжениях ниже предела текучести.

Разрушение происходит без заметных пластических деформаций, имеет хрупкий характер (см. выше). Это наблюдается в подкрановых балках, балках рабочих площадок при загружении их подвижным составом, элементы бункерных эстакад, башни и мачты, испытывающие многократные воздействие порывов ветра и т.п.

Поэтому расчет на усталость следует вести по первому предельному состоянию, т.е.

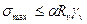(2.21)

при ограничении

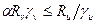, при 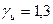, (2.22)

где 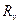- условное расчетное сопротивление усталости, зависящее от типа стали и степени концентрации напряжений в проверяемой точке конструкции; 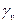- условный коэффициент усталости; 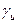= 1,3 - коэффициент надежности по временному сопротивлению.