Измерение частот и фаз методом фигур Лиссажу
Измерение методом фигур Лиссажу основано на анализе осциллограммы, получающейся при сложении двух взаимно перпендикулярных гармонических колебаний электронного луча.
Для измерения частоты колебаний на вход вертикального отклонения подают переменное напряжение неизвестной частоты, а на вход усилителя горизонтального отклонения – опорное напряжение, частота которого известна. При выполнении условия кратности частоты опорного напряжения частоте исследуемого сигнала на экране осциллографа наблюдается неподвижная осциллограмма, которая для гармонических колебаний представляет собой одну из фигур Лиссажу. На рисунке 6 приведены некоторые фигуры Лиссажу для разных отношений частоты колебания опорного напряжения к частоте колебания исследуемого напряжения N.
Практически, для измерения частот колебаний плавно изменяют частоту колебаний опорного напряжения до тех пор, пока осциллограмма не станет соответствовать фигуре Лиссажу первого порядка, которая представляет собой эллипс. При разности фаз 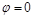 или
или 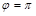 эллипс вырождается в отрезок прямой, а при
эллипс вырождается в отрезок прямой, а при 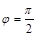 и равенстве амплитуд – в
и равенстве амплитуд – в 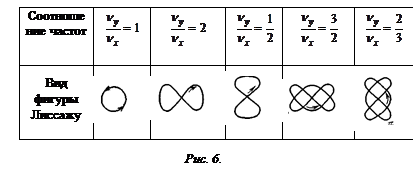 окружность. Во всех этих случаях частота исследуемого напряжения равняется частоте опорного напряжения.
окружность. Во всех этих случаях частота исследуемого напряжения равняется частоте опорного напряжения.
 Для измерения сдвига фаз между двумя напряжениями одной и той же частоты на вход вертикального отклонения подается одно из них, а на вход горизонтального отклонения – другое.
Для измерения сдвига фаз между двумя напряжениями одной и той же частоты на вход вертикального отклонения подается одно из них, а на вход горизонтального отклонения – другое.
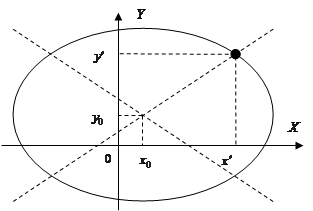
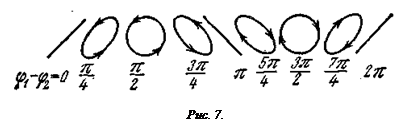 Поскольку частоты обоих напряжений одинаковы, то на экране будет изображение фигуры Лиссажу первого порядка, информация о сдвиге фаз содержится в ее форме (рисунок 7).
Поскольку частоты обоих напряжений одинаковы, то на экране будет изображение фигуры Лиссажу первого порядка, информация о сдвиге фаз содержится в ее форме (рисунок 7).
Проанализируем форму фигуры Лиссажу первого порядка. Зависимости отклонений по координатам 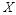 и
и 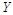 имеют вид:
имеют вид:
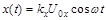
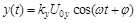 , (1)
, (1)
где 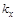 и
и 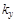 – коэффициенты пропорциональности между напряжениями, поданными на входы
– коэффициенты пропорциональности между напряжениями, поданными на входы 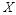 и
и 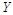 , и отклонениями луча в этих направлениях;
, и отклонениями луча в этих направлениях; 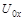 и
и 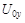 амплитуды гармонических напряжений.
амплитуды гармонических напряжений.
Введя обозначения: 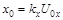 и
и 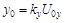 амплитуд отклонений луча по координатам
амплитуд отклонений луча по координатам 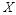 и
и 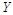 соответственно, получим:
соответственно, получим:
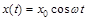
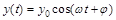 . (2)
. (2)
Используя формулы тригонометрии:
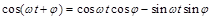 и
и 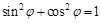 ,
,
можно записать:
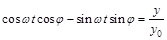 , (1)
, (1)
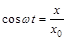 , (2)
, (2)
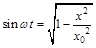 . (3)
. (3)
Подставив (2) и (3) в (1), получим:
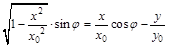 . (3)
. (3)
Возведя обе части уравнения в квадрат и выполнив преобразования, окончательно получим:
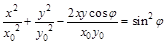 . (4)
. (4)
Из последней формулы следует, что:
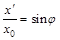 , где
, где 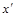 – отклонение по оси
– отклонение по оси 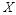 при
при 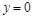 , (5)
, (5)
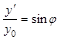 , где
, где 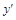 – отклонение по оси
– отклонение по оси 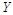 при
при 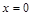 . (6)
. (6)
Смысл 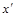 ,
, 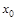 ,
, 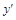 ,
, 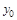 можно понять из рисунка 7.
можно понять из рисунка 7.


Дата добавления: 2015-03-03; просмотров: 1785;
