Стаціонарний потенціал Гольдмана-Ходжкіна-Катца
Розбіжності між експериментальними значеннями потенціалу спокою на мембрані і розрахованими за рівнянням Нернста для рівноважного потенціалу (див. рис. 6.32) пов'язані насамперед з тим, що мембрана проникна не лише для іонів К+, а й для інших іонів. Наявність сумарного потоку для цих іонів спричинює виникнення мембранної різниці потенціалів, яка починає гальмувати транспорт іонів, внаслідок чого сумарний
електричний струм іонів 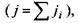 а отже, і сумарний потік іонів
а отже, і сумарний потік іонів  припиняється. При цьому на мембрані встановлюється різниця потенціалів, спричинена не умовою рівноваги
припиняється. При цьому на мембрані встановлюється різниця потенціалів, спричинена не умовою рівноваги 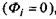 , а умовою стаціонарності, яка означає, що повний потік, зумовлений потоками всіх іонів, дорівнює нулю
, а умовою стаціонарності, яка означає, що повний потік, зумовлений потоками всіх іонів, дорівнює нулю 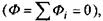 при цьому кожний з потоків у загальному випадку відмінний від нуля
при цьому кожний з потоків у загальному випадку відмінний від нуля 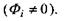
Саме цим стаціонарний потенціал відрізняється від рівноважного потенціалу Нернста, умовою виникнення якого є рівність нулеві потоку лише одного певного сорту іонів.
У теорії стаціонарного потенціалу, розвиненої Д. Гольдманом, А. Ходжкіним і Б. Катцем, враховувалися внески в сумарний потік лише одновалентних іонів натрію, калію і хлору.
Розраховуючи мембранний потенціал, що виникає за цих  умов, автори виходили з таких положень:
умов, автори виходили з таких положень:
1) здійснюється умова стаціонарності

2) у мембрані спостерігається сталість градієнта електричного потенціалу

3) потік кожного сорту іонів підпорядковується рівнянню Нернста-Планка
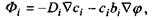 (4.57)
(4.57)
де 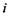 - індекс сорту іонів,
- індекс сорту іонів, 
Інтегрування рівнянь (4.57) з урахуванням умови стаціонарності 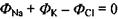 дає змогу одержати такий вираз для мембранного потенціалу (див. деталі нижче):
дає змогу одержати такий вираз для мембранного потенціалу (див. деталі нижче):
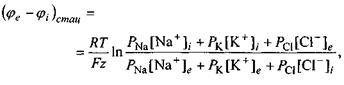 (4.58)
(4.58)
де 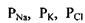 - проникності мембрани для відповідних іонів. Це і є формула для стаціонарного потенціалу Гольдмана-Ходжкіна-Катца, яку ще називають рівнянням Гольдмана. Це рівняння значно краще узгоджується з експериментальними даними, ніж рівняння Нернста (див. рис. 4.32). Легко переконатись, що рівняння Нернста є частинним випадком рівняння Гольдмана. Дійсно, в спокої у гігантському аксоні кальмара
- проникності мембрани для відповідних іонів. Це і є формула для стаціонарного потенціалу Гольдмана-Ходжкіна-Катца, яку ще називають рівнянням Гольдмана. Це рівняння значно краще узгоджується з експериментальними даними, ніж рівняння Нернста (див. рис. 4.32). Легко переконатись, що рівняння Нернста є частинним випадком рівняння Гольдмана. Дійсно, в спокої у гігантському аксоні кальмара 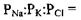
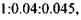 тобто
тобто 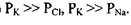
У цьому випадку 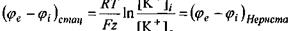 для іонів
для іонів 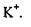
Вираз для стаціонарного мембранного потенціалу можна одержати, використовуючи безрозмірний мембранний потенціал 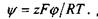 Для цього дещо перетворимо рівняння Нернста-Планка, використавши умову сталості градієнта потенціалу в мембрані
Для цього дещо перетворимо рівняння Нернста-Планка, використавши умову сталості градієнта потенціалу в мембрані
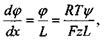
де  - товщина мембрани, а саме:
- товщина мембрани, а саме:
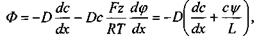
звідки
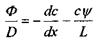
або
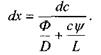 (4.59)
(4.59)
Проінтегруємо рівняння (4.59) по всій товщині мембрани
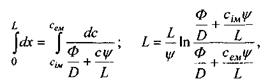
звідки
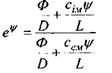
або
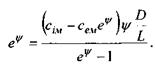 (4.60)
(4.60)
Оскільки 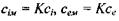 (див. рис. 4.24), то рівняння (4.60) набуває вигляду
(див. рис. 4.24), то рівняння (4.60) набуває вигляду
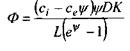
або
 (4.61)
(4.61)
де 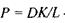 - проникність мембрани.
- проникність мембрани.
Одержимо вираз для стаціонарного мембранного потенціалу, що виникає при наявності потоку іонів 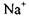 у клітину, потоку іонів
у клітину, потоку іонів 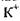 зовні і потоку іонів
зовні і потоку іонів 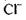 у клітину. Зробимо це поки що без урахування
у клітину. Зробимо це поки що без урахування 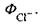 За умови, що загальний потік
За умови, що загальний потік  , маємо
, маємо
 (4.62)
(4.62)
Використовуючи (4.61), з умови (4.62) отримаємо
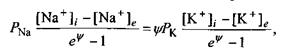
звідки
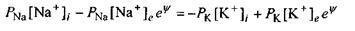
або
 (4.63)
(4.63)
З урахуванням того, що 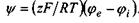 , з (4.63) маємо
, з (4.63) маємо
 . (4.64)
. (4.64)
Враховуючи внесок потоку іонів хлору, одержимо з (4.64) вираз (4.58):
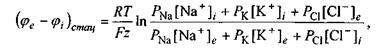
тобто шукану формулу для стаціонарного потенціалу.
Дата добавления: 2015-03-03; просмотров: 3445;
