Перенос молекул (атомов) через мембраны.Уравнение Фика

Важным элементом функционирования мембран является их способность пропускать или не пропускать молекулы (атомы) и ионы. Существенно, что вероятность такого проникновения частиц зависит как от направления их перемещения, например в клетку или из клетки, так и от разновидности молекул и ионов.

Эти вопросы рассматриваются в разделе физики, относящемся - к явлениям переноса. Таким термином называют необратимые F, процессы, в результате которых в физической системе происходит пространственное перемещение (перенос) массы, импульса, энергии, заряда или какой-либо другой физической величины.

К явлениям переноса относят диффузию (перенос массы вещества), вязкость (перенос импульса), теплопроводность (перенос энергии), электропроводность (перенос электрического заряда). Здесь и в следующих параграфах рассматриваются наиболее существенные для биологических мембран явления: перенос вещества и перенос заряда. Как синоним переноса частиц в биофизике широкое распространение получил также термин транспорт частиц.

Выведем основное уравнение диффузии (уравнение Фика), рассматривая процесс переноса в жидкостях.

Пусть через некоторую площадку S (рис. 11.10) во всех направлениях перемещаются молекулы жидкости. Учитывая теорию : молекулярного строения жидкости (см. § 7.6), можно сказать, что молекулы пересекают площадку, перескакивая из одного положения равновесия в другое.

На расстояниях, равных среднему перемещению 5 молекул (среднее расстояние между молекулами жидкости), вправо и влево от площадки построим прямоугольные параллелепипеды небольшой толщины l (l <<δ). Объем каждого параллелепипеда равен Sl. Если п — концентрация молекул, то внутри

выделенных параллелепипедов имеется Sin молекул. Предположим, что концентрация молекул изменяется в пространстве, в левом (1) выделенном параллелепипеде концентрация равна n₁а в правом (2) — п₂. Следовательно, в одном параллелепипеде SZn_x молекул, а в другом - Sln₂ молекул.

Все молекулы вследствие хаотичного их движения можно условно представить шестью группами, каждая из которых перемещается вдоль или против направления одной из осей координат. Отсюда следует, что в направлении, перпендикулярном площадке S, вдоль оси ОХот первого параллелепипеда перескакивает ¹/₆ Sln₁ молекул, а противоположно оси ОХ от второго параллелепипеда перескакивает ¹/₆ Sln₂ молекул.

Время Δt «пролета» этими молекулами площадки S может быть найдено следующим образом. Предположим, что все молекулы из выделенных объемов движутся с одинаковыми средними скоростями <v>. Тогда молекулы в объеме 1 или 2, дошедшие до площадки S, пересекают ее в течение промежутка времени

Подставляя в (11.1)выражение для средней скорости ύ из (7.20), получаем

Δt=(l/δ)*τ (11.2)

где т — среднее время «оседлой жизни» молекулы, оно может рассматриваться как среднее время перескока. «Баланс» переноса молекул через площадку S за промежуток времени Δt равен

Умножая (11.3)на массу тотдельной молекулы и деля на Δt, находим массовый поток сквозь площадку S:

т. е. масса вещества, которая за 1 с переносится через площадку S. Изменение концентрации п₂ - п₁ молекул можно представить как произведение dn/dxна расстояние 2δ между выделенными объемами:

В уравнении (11.4) заменим Δt согласно (11.2)и (п₂ - п₁) согласно (11.5):

Отношение потока к площади S, через которую он переноситься, называется плотностью потока:

Произведение массы молекулы на их концентрацию есть плотность вещества (парциальная плотность):

Это есть уравнение диффузии (уравнение Фика), которое обычно записывают в виде:

Знак «-» показывает, что суммарная плотность потока вещества при диффузии направлена в сторону уменьшения плотности (в сторону, противоположную градиенту плотности), D — коэффициент диффузии, применительно к рассмотренному примеру диффузии в жидкости он равен

Как видно из (11.10),единица измерения коэффициента диффузии [м²/с].

Уравнение диффузии можно записать не только для плотности
массового потока кг/(м²*с), но и для плотности потока частиц 1/(м²*с) и плотности потока вещества моль/(м²*с), при этом в уравнении (11.9) вместо градиента плотности следует использовать соответственно градиент концентрации 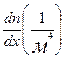или градиент молярной концентрации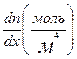

А. Эйнштейн показал, что коэффициент диффузии пропорционален температуре:

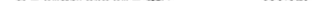И поэтому вместо (11.11) имеем

В формуле (11.12) и далее и_т — подвижность диффундирующих молекул (частиц), выраженная для моля. Вообще говоря, подвижностью диффундирующей частицы (молекулы, атома, иона, электрона) и называют коэффициент пропорциональности между скоростью v частицы и силой f, двигающей частицу, в том случае, когда на частицу не действуют другие силы (например, трение или соударение с другими частицами) и она перемещается равномерно:

Как видно из (11.14), единица подвижности 1 м/(с • Н). Величины u_m и u связаны через постоянную Авогадро:

Преобразуем уравнение (11.9) применительно к биологической мембране. Будем считать, что концентрация частиц, диффундирующих через мембрану, изменяется в мембране по линейному закону (рис. 11.11). Молярные концентрации частиц внутри и вне клетки соответственно равны c_i и с₀. Молярная концентрация этих же частиц в мембране изменяется от внутренней к наружной ее части соответственно от с_mi до с_м0. Учитывая линейное изменение концентрации молекул, запишем

где I — толщина мембраны, тогда вместо (11.11) имеем

Практически доступнее определить молярные концентрации частиц не внутри мембраны (c_Mi и с_м0), а вне мембраны: в клетке (с_i) и снаружи клетки (с₀). Считают, что отношение граничных значенийконцентраций в мембране равно отношению концентраций в прилегающих к мембране слоях: с_м0/с_Mi = c_o/c_i, откуда

где k — коэффициент распределения вещества (частиц) между мембраной и окружающей средой (обычно водная фаза). Из (11.18) следует

Подставляя (11.19) в (11.17), имеем

Пусть

где Р — коэффициент проницаемости. В результате получаем уравнение для плотности потока вещества при диффузии через биологическую мембрану:

Уравнение Нернста—Планка. Перенос ионов через мембраны

Как известно, на мембране существует разность потенциалов, следовательно, в мембране имеется электрическое поле. Оно оказывает влияние на диффузию заряженных частиц (ионов и электронов). Между напряженностью поля Е и градиентом потенциала dφ/dx существует известное соотношение (см. § 12.1):

Заряд иона равен Ze. На один ион действует сила f=Ze(dφ/dx); сила, действующая на 1 моль ионов, равна

где F — постоянная Фарадея, F = eN_A.

Скорость направленного движения ионов пропорциональна действующей силе [см. (11.4), (11.5)]:

Чтобы найти поток вещества (ионов), выделим объем электролита (рис. 11.12) в виде прямоугольного параллелепипеда с ребром, численно равным скорости ионов. Все ионы, находящиеся в параллелепипеде, за 1 с пройдут через площадку S. Это и будет поток Ф. Число молей этих ионов

можно найти, умножая объем параллелепипеда (vS) на молярную концентрацию ионов с:

Плотность потока вещества найдем, используя формулы (11.24) и (11.25):

В общем случае перенос ионов определяется двумя факторами: неравномерностью их распределения, т. е. градиентом концентрации [см. (11.11)], и воздействием электрического поля [см. (11.26)]:

Это уравнение Нернста—Планка. Используя выражение для подвижности (11.12), преобразуем уравнение (11.27) к виду

Это другая форма записи уравнения Нернста—Планка

Используем уравнение Нернста—Планка для установления зависимости плотности диффузионного потока от концентрации ионов и от напряженности электрического поля. Предположим, система находится в стационарном состоянии, т. е. плотность потока Jпостоянна. Электрическое поле в мембране примем за однородное, следовательно, напряженность поля одинакова, а потенциал линейно изменяется с расстоянием. Это позволит считать, что 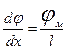, где φ_м — разность потенциалов на мембране.

Упростим запись слагаемого в уравнении (11.28):

где

— — —

вспомогательная величина (безразмерный потенциал). С учетом (11.29) получим уравнение Нернста—Планка в виде

Разделим переменные и проинтегрируем уравнение:

Потенцируя (11.31), получаем

откуда

Преобразуем формулу (11.32), учитывая выражения (11.19) и (11.20):

Вообще говоря, формула (11.33) справедлива как для положительных (Z > 0, у > 0), так и для отрицательных {Z < 0, ψ < 0) ионов. Однако для отрицательных ионов целесообразно видоизменить это выражение, подставив в него отрицательное значение безразмерного потенциала:

Разделим числитель и знаменатель этого выражения на е^-ψ:

При использовании этой формулы необходимо помнить, что отрицательные значения Z и ψ уже учтены в самой формуле, т. е. ψ— положительная величина.

Уравнения (11.33) и (11.34) устанавливают связь плотности стационарного потока ионов с тремя величинами: 1) проницаемостью мембран для данного иона, которая характеризует взаимодействие мембранных структур с ионом; 2) электрическим полем; 3) молярной концентрацией ионов в водном растворе, окружающем мембрану {с_i и с₀).

Проанализируем частные случаи уравнения (11.33):

а) ψ = 0, что означает либо Z = 0 (нейтральные частицы), либо отсутствие электрического поля в мембране (φ_м = 0), либо и то, и другое:

Найдем пределы отдельных сомножителей.

1. 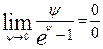Эту неопределенность можно раскрыть по правилу Лопиталя:

2.Отсюда получаем, как и следовало ожидать, уравнение (11.21):

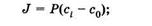
б) одинаковая молярная концентрация ионов по разные стороны от мембраны (c_i = с₀ = с) при наличии электрического поля:

Это соответствует электропроводимости в электролите (см. § 12.9). Для нейтральных частиц (Z = 0 и ψ=0) J = 0;

в) если мембрана непроницаема для частиц (Р = 0), то, естественно, плотность потока равна нулю.

<56 57 585960 61 62 >

Дата добавления: 2015-03-03; просмотров: 1222;