Механические свойства твердых тел
Изменение взаимного расположения точек тела, которое приводит к изменению его формы и размеров, называют деформацией. Деформации могут быть вызваны внешними воздействиями (механическими, электрическими или магнитными) или изменение температуры тела. Здесь рассматриваются деформации, возникающие при действии сил на тело.
В твердых телах деформацию называют упругой, если после прекращения действия силы она исчезает. Если же деформация сохраняется и после прекращения внешнего воздействия, то ее называют пластической. Промежуточный случай, т, е. неполное исчезновение деформации, принято называть упругопластической деформацией.
Наиболее простым видом деформации является растяжение (сжатие). Оно, например, возникает в стержне (рис. 8.11) при действии силы, направленной вдоль его оси. Если стержень длинной I при этом удлинился на ∆1, то е = ∆l/l является мерой деформации растяжения и называется относительным удлинением. Другим видом деформации является сдвиг (рис. 8.12).
Сила, касательная к одной из граней прямоугольного параллелепипеда,
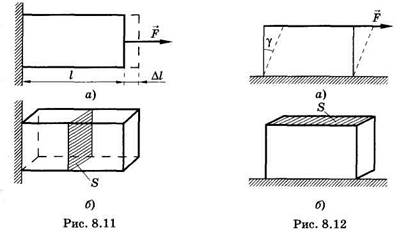
вызывает его деформацию, превращая в косоугольный параллелепипед (см. штриховые линии на рисунке). Угол у называют углом сдвига, a tg γ — относительным сдвигом. Так как обычно угол у мал, то можно считать tg γ = γ.
При действии на тело внешней деформирующей силы расстояние между атомами (ионами) изменяется. Это приводит к возникновению внутренних сил, стремящихся вернуть атомы (ионы) в первоначальные положения. Мерой этих сил является механическое напряжение (или просто напряжение).
Непосредственно напряжение не измеряется. В ряде случаев его можно вычислить через внешние силы, действующие на тело. Косвенно напряжение можно определить по некоторым физическим эффектам (см., например, § 20.5).
Применительно к деформации растяжения напряжение а можно выразить как отношение силы к площади поперечного сечения стержня (см. рис. 8.11, б):
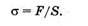
Для деформации сдвига напряжение т выражают как отношение силы к площади грани, к которой сила касательна (см. рис. 8.12, б). В этом случае τ называют касательным напряжением:
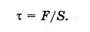
Упругие деформации подчиняются закону Гука, согласно которому напряжение пропорционально деформации. Для двух рассмотренных случаев (растяжение-сжатие и сдвиг) это аналитически записывается так:

где Е — модуль Юнга, a G — модуль сдвига.
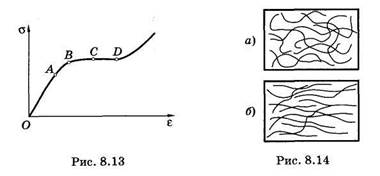
Экспериментальная кривая растяжения приведена на рис. 8.13. Участок ОА соответствует упругим деформациям, точка В — пределу упругости, характеризующему то максимальное напряжение, при котором еще не имеют места деформации, остающиеся в теле после снятия напряжения (остаточные деформации). Горизонтальный участок CD кривой растяжения соответствует пределу текучести — напряжению, начиная с которого деформация возрастает без увеличения напряжения. И наконец, напряжение, определяемое наибольшей нагрузкой, выдерживаемой перед разрушением, является пределом прочности.
Между упругими свойствами кристаллических мономеров и полимерных материалов существует огромная и принципиальная разница, например, в пределах прочности сталь разрывается уже
при растяжении на 0,3%, а мягкие резины можно растягивать до,300%. Это связано с качественно другим механизмом упругости высокомолекулярных соединений.
Как уже говорилось, при деформации кристаллических твердых тел, например стали, силы упругости всецело определяются, изменением межатомных расстояний. Структура высокомолекулярных соединений не регулярна. Они состоят из очень длинных гибких молекул, которые причудливо изогнуты, части молекул находятся в хаотическом тепловом движении так, что их форма и длина все время изменяются. Но в каждый данный момент большинство молекул в недеформированном образце имеет длину, близкую к наиболее вероятной. При приложении нагрузки к материалу (рис. 8.14, а) его молекулы выпрямляются в соответствующем направлении и длина образца увеличивается (рис. 8.14, б). После снятия нагрузки вследствие хаотического теплового движения длина каждой молекулы восстанавливается и образец укорачивается.
Упругость, свойственную полимерам, называют каучукоподобной эластичностью (высокой эластичностью или высокоэластичностью).
Приведем данные по механическим свойствам некоторых материалов (табл. 16).
Таблица 16
| Материал | Модуль Юнга, ГПа | Предел прочности, МПа |
| Сталь Капрон стеклонаполненный Органическое стекло | 3,5 |
Различие между деформацией кристаллических мономеров и полимерных материалов проявляется и во временной ее зависимости. Дело в том, что практически все материалы обладают ползучестью: под действием постоянной нагрузки происходит их деформация. В полимерах распрямление молекул при нагрузке материала и скольжение макромолекул происходят более длительно, чем, например, ползучесть в металлах. В какой-то мере при ползучести процессы, происходящие в полимере, соответствуют течению вязкой жидкости. Сочетание вязкого течения и высокой эластичности позволяет называть деформацию, характерную для полимеров, вязкоупругой.
Упругие и вязкие свойства тел удобно моделировать. Это дает возможность нагляднее представить механические свойства биологических объектов (см. § 8.4).
В качестве модели упругого тела (упругой деформации) выберем пружину (рис. 8.15, а), малая деформация которой соответствует закону Гука.
Моделью вязкого тела является поршень с отверстиями, движущийся в цилиндре с вязкой жидкостью (рис. 8.15, б).
 |
 Силу сопротивления среды в этом случае примем пропорциональной скорости перемещения поршня [см. (5.16)]:
Силу сопротивления среды в этом случае примем пропорциональной скорости перемещения поршня [см. (5.16)]:
Преобразуем уравнение (8.2), основываясь на аналогии. Вместо силы сопротивления запишем напряжение (Fconp → σ), т. е. силу, отнесенную к единице площади, коэффициент трения, характеризующий свойство среды оказывать сопротивление движущемуся в ней телу, заменим коэффициентом вязкости среды (r → η), смещение тела — относительным удлинением (x → ε). Тогда вместо (8.2) получим связь между скоростью вязкой деформации и напряжением:
 |
В справедливости (8.3) частично можно убедиться проверкой размерностей: σ [Па], η[Па • с], dε/dt[с-1]. Из (8.3) видно, что напряжение зависит не от самой деформации, а от ее скорости (скорости перемещения поршня).
Вязкоупругие свойства тел моделируются системами, состоящими из различных комбинаций двух простых моделей: пружина и поршень. Рассмотрим некоторые из них.
Наиболее простой системой, сочетающей упругие и вязкие свойства, является модель Максвелла, в которой последовательно соединены упругий и вязкий элемент (рис. 8.15, в).
При воздействии постоянной силой пружина упруго мгновенно удлиняется до значения, определяемого законом Гука, а поршень движется с постоянной скоростью до тех пор, пока действует сила (напряжение). Так реализуется на модели ползучесть материалa.
Если быстро растянуть модель Максвелла и закрепить это состояние, то деформация будет сохраняться. Пружина после быстрого растяжения начнет сокращаться, вытягивая поршень. Со временем будет происходить релаксация, т. е. уменьшение (расслабление) напряжения.
 |
Опишем математически эту модель. Из закона Гука (8.1) следует εупр = σ/E, где εупр — упругая часть общей деформации в модели Максвелла. Скорость этой деформации равна
Скорость вязкой деформации выразим из (8.3):
 |
 |
Суммируя (8.4) и (8.5), находим скорость общей (суммарной) деформации модели Максвелла:
Из уравнения (8.6) можно получить временные зависимости как деформации, так и напряжения.
Если σ= const и dσ/dt = 0 (постоянная сила приложена к модели), то из (8.6) следует
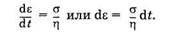
 |
Интегрируя последнее выражение от начального момента времени и нулевой деформации до текущих значений t и ε, получаем
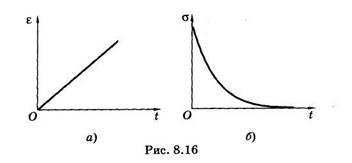
Это соответствует ползучести (рис. 8.16, а).
Если ε = const и dε/dt = 0 (поддерживается постоянная деформация), то из (8.6) следует
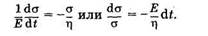
Интегрируя последнее выражение от начального момента времени и начального напряжения σ0 до текущих значений t и σ, получаем:
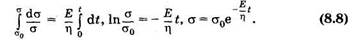
Это соответствует релаксации напряжения (рис. 8.16, б).
В рамках модели Максвелла под действием нагрузки происходит, как было показано, быстрое (мгновенное) первоначальное упругое растяжение. В реальных полимерах вязкоупругая деформация обычно происходит сразу же после приложения нагрузки. Поэтому более подходящей может оказаться модель Кельвина — Фойхта, состоящая из параллельно соединенных пружины и поршня, нечто вроде амортизатора в автомашине (см. рис. 8.15, г).
Если мгновенно создать в такой системе напряжение

приложив постоянную силу, то деформация системы будет возрастать. Используя (8.1) и (8.3), преобразуем (8.9):
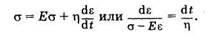
Проинтегрируем последнее выражение от начального момента времени и нулевой  деформации до текущих значений t и ε:
деформации до текущих значений t и ε:
 |
 |
Потенцируя, имеем
Как видно, в рамках модели Кельвина—Фойхта деформация экспоненциально возрастает со временем. При снятии нагрузки (σ = 0 в момент t1 деформация начнет экспоненциально убывать. Оба эти случая показаны на рис. 8.17.
В полимерах реализуются разные виды деформации: упругая обратимая (модель — пружина), вязкоупругая обратимая (модель Кельвина—Фойхта) и необратимая вязкая (модель — поршень). Сочетание этих трех элементов позволяет создавать модели, наиболее полно отражающие механические свойства тел и, в частности, биологических объектов.
Моделирование механических свойств тел широко используется в реологии. Основная задача реологии — это выяснение зависимости напряжения от относительной деформации: σ = f(ε); напряжения от времени (релаксация напряжения): σ = f(t) при ε = const; относительной деформации от времени (ползучесть): ε = f(t) при σ = const.
Дата добавления: 2015-03-03; просмотров: 1979;
