Пульсовая волна

При сокращении сердечной мышцы (систола) кровь выбрасыва­ется из сердца в аорту и отходящие от нее артерии. Если бы стенки этих сосудов были жесткими, то давление, возникающее в крови на выходе из сердца, со скоростью звука передалось бы к перифе­рии. Упругость стенок сосудов приводит к тому, что во время сис­толы кровь, выталкиваемая сердцем, растягивает аорту, артерии и артериолы, т. е. крупные сосуды воспринимают за время систолы больше крови, чем ее оттекает к периферии. Систолическое давле­ние человека в норме равно приблизительно 16 кПа. Во время рас­слабления сердца (диастола) растянутые кровеносные сосуды спа­дают и потенциальная энергия, сообщенная им сердцем через кровь, переходит в кинетическую энергию тока крови, при этом поддерживается диастолическое давление, приблизительно равное 11 кПа.

Распространяющуюся по аорте и артериям волну повышенного давления, вызванную выбросом крови из левого желудочка в пе­риод систолы, называют пульсовой волной.

Пульсовая волна распространяется со скоростью 5—10 м/с и даже более. Следовательно, за время систолы (около 0,3 с) она

должна распространиться на расстоя­ние 1,5—3 м, что больше расстояния от сердца к конечностям. Это означает, что начало пульсовой волны достигнет конечностей раньше, чем начнется спад давления в аорте. Профиль части арте­рии схематически показан на рис. 9.6: а — после прохождения пульсовой вол­ны, б — в артерии начало пульсовой волны, в — в артерии пульсовая волна, г — начинается спад повышенного дав­ления.

Д1ульсовой волне будет соответство­вать пульсирование скорости кровото­ка в крупных артериях, однако ско­рость крови (максимальное значение

0,3—0,5 м/с) существенно меньше скорости распространения пульсовой волны.

Из модельного опыта и из общих представлений о работе серд­ца ясно, что пульсовая волна не является синусоидальной (гармо­нической). Как всякий периодический процесс, пульсовая волна может быть представлена суммой гармонических волн (см. § 5.4). Поэтому уделим внимание, как некоторой модели, гармониче­ской пульсовой волне.

Предположим, что гармоническая волна [см. (5.48)] распрост­раняется по сосуду вдоль оси X со скоростью v. Вязкость крови и упруговязкие свойства стенок сосуда уменьшают амплитуду вол­ны. Можно считать (см., например, § 5.1), что затухание волны будет экспоненциальным. На основании этого можно записать следующее уравнение для пульсовой волны:

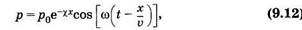
где р₀ — амплитуда давления в пульсовой волне; х — расстояние до произвольной точки от источника колебаний (сердца); t — вре­мя; ω — круговая частота колебаний; χ — некоторая константа, определяющая затухание волны. Длину пульсовой волны можно найти из формулы

Волна давления представляет некоторое «избыточное» давле­ние. Поэтому с учетом «основного» давления р_а (атмосферное давление или давление в среде, окружающей сосуд) можно измене­ние Явления записать следующим образом:

Как видно из (9.14), по мере продвижения крови (по мере уве­личения х) колебания давления сглаживаются. Схематично на рис. 9.7 показано колебание давления в аорте вблизи сердца (а) и в артериолах (б). Графики даны в предположении модели гармо­нической пульсовой волны.

На рис. 9.8 приведены экспериментальные графики, показы­вающие изменение среднего значения давления и скорости v_кр кровотока в зависимости от типа кровеносных сосудов. Гидроста­тическое давление крови не учитывается. Давление — избыточ­ное над атмосферным. Заштрихованная область соответствует ко­лебанию давления (пульсовая волна).

Скорость пульсовой волны в крупных сосудах следующим об­разом зависит от их параметров (формула Моенса—Кортевега):

где Е — модуль упругости, р — плотность вещества сосуда, h — толщина стенки сосуда, d — диаметр сосуда.

У человека с возрастом модуль упругости сосудов возрастает, поэтому, как следует из (9.15), становится больше и скорость пульсовой волны.