Основные проблемы и понятия метрологии
Активный транспорт — перенос молекул и ионов, который происходит с затратой химической энергии в направлении от меньших значений величин к большим.
При этом нейтральные молекулы переносятся в область большей концентрации, а ионы переносятся против сил, действующих на них со стороны электрического поля. Таким образом, активным транспортом осуществляется перенос веществ в направлении, противоположном транспорту, который должен был бы происходить под действием градиентов (прежде всего концентрационного и электрического). Энергия получается за счет гидролиза молекул особого химического соединения — аденозинтрифосфорной кислоты (АТФ). Экспериментально установлено, что энергии распада одной молекулы АТФ достаточно для выведения наружу трех ионов натрия и введения внутрь клетки двух ионов калия. Схема активного транспорта представлена на рис.13.
Захватив одним активным центром ион калия из наружной среды, а другим ион натрия — из внутренней, система, потребляя АТФ, поворачивается внутри мембраны на 180°. Ион натрия оказывается вне клетки и там отделяется, а ион калия попадает внутрь и тоже освобождается, после чего молекула белка принимает исходное положение, и все начинается сначала.
За счет активного транспорта клетка поддерживает внутри себя высокую концентрацию калия и низкую концентрацию натрия. При этом ионы могут перемещаться против градиента их концентрации (аналогия с газом: перекачивание газа из сосуда с низким давлением в сосуд с высоким давлением).
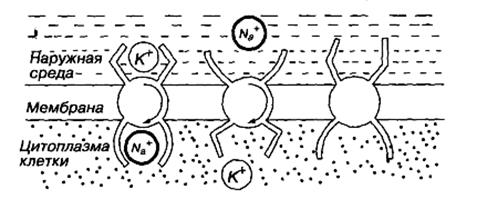
Рис.13. Схема активного транспорта
Активный транспорт веществ через биологические мембраны имеет огромное значение. За счет активного транспорта в организме создаются градиенты концентраций, градиенты электрических потенциалов, градиенты давления и т.д., поддерживающие жизненные процессы, т. е., с точки зрения термодинамики, активный перенос удерживает организм в неравновесном состоянии, поддерживает жизнь.
Существование активного транспорта веществ через биологические мембраны впервые было доказано в опытах Уссинга (1949 г.) на примере переноса ионов натрия через кожу лягушки (рис.14).
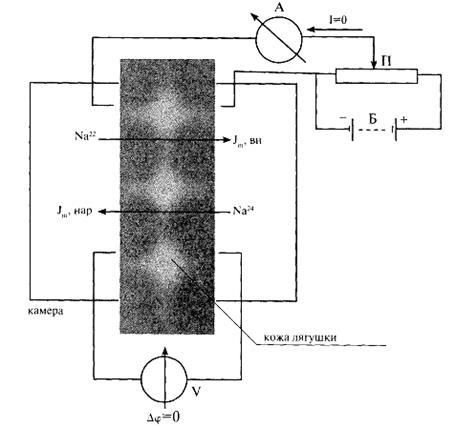
Рис. 14. Схема опыта Уссинга (А — амперметр, V — вольтметр, Б — батарейка, П — потенциометр)
Экспериментальная камера Уссинга, заполненная нормальным раствором Рингера, была разделена на две части свежеизолированной кожей лягушки. На рис.14 слева — наружная мукозная поверхность кожи, справа — внутренняя серозная. Наблюдались потоки ионов натрия через кожу лягушки: слева направо от наружной к внутренней поверхности и справа налево — от внутренней к наружной поверхности.
На коже лягушки, разделяющей раствор Рингера, возникала разность потенциалов, причем внутренняя сторона кожи имела положительный потенциал по отношению к наружной. В установке имелся блок компенсации напряжения, с помощью которого устанавливалась разность потенциалов на коже лягушки, равная нулю, что контролировалось вольтметром. Кроме того, поддерживалась одинаковая концентрация ионов с наружной и внутренней стороны. При этих условиях, если бы перенос ионов натрия через кожу лягушки определялся только пассивным транспортом, то потоки ионов натрия должны были бы быть равны друг другу, а ток в цепи отсутствовать.
Однако было обнаружено, что в условиях опыта (отсутствие градиентов электрического потенциала и концентрации) через кожу лягушки течет электрический ток, следовательно, происходит односторонний перенос заряженных частиц. Установлено, что ток через кожу течет от внешней среды к внутренней. Методом меченых атомов было показано, что поток натрия внутрь больше, чем поток наружу.
Для этого в левый раствор экспериментальной камеры были включены радиоактивные изотопы Na22, а в правый — Na24. Изотоп Na22 распадается с излучением жестких γ-квантов. Распад Na24 сопровождается мягким β-излучением. Регистрация γ - и β - излучений показала, что поток Na22 больше потока Na24. Эти экспериментальные данные неопровержимо свидетельствовали о том, что перенос ионов натрия через кожу лягушки не подчиняется уравнению пассивного транспорта. Следовательно, имеет место активный перенос. Дальнейшие опыты показали, что истощение запасов АТФ в коже лягушки приводит к полной остановке однонаправленного потока ионов натрия.
3. Цель деятельности студентов на занятии:
Студент должен знать:
1. Роль мембраны в функционировании клетки.
2. Структуру, строение и модели мембран.
3. Функции мембраны.
4. Физические свойства мембран.
5. Уравнение Фика.
6. Уравнение Нернста-Планка.
7. Виды пассивного транспорта частиц через мембрану.
8. Активный транспорт частиц через мембрану.
Студент должен уметь:
1. Объяснять строение мембраны.
2. Объяснять искусственные модели мембран.
3. Объяснять механизм пассивного транспорта через мембрану.
4. Объяснить механизм активного транспорта через мембрану.
5. Решать ситуационные задачи.
4. Содержание обучения:
1. Строение биологических мембран.
2. Жидко-мозаичная модель мембраны.
3.Искусственные модели мембран.
4. Основные функции клеточной мембраны.
5. Физические свойства мембран.
6. Перенос молекул (атомов) через мембрану. Уравнение Фика.
7. Перенос ионов через мембраны. Уравнение Нернста-Планка.
8. Разновидности пассивного переноса молекул и ионов через мембраны.
9. Активный транспорт. Опыт Уссинга.
10. Решение ситуационных задач.
5.Перечень вопросов для проверки исходного уровня знаний:
1. Что представляют собой биологические мембраны?
2. Что является основой мембраны?
3. Для чего используют физико-химические ( искусственные) модели мембраны?
4. Опишите жидко-мозаичную модель мембраны.
5. Что такое латеральная диффузия? флин-флоп переход?
6. Какие основные функции выполняет мембрана и в чем они заключаются?
7. Запишите уравнения Фика и Нернста-Планка. Какие процессы они описывают?
8. Что называется подвижностью?
9. Что такое пассивный транспорт? Какие разновидности пассивного транспорта существуют?
10. Что такое активный транспорт? За счет чего он осуществляется?
11. Какое значение имеет активный транспорт веществ?
12. Объясните явления переноса вещества и заряда через мембрану.
13. Что будет, если клетку поместить в чистую воду?
6. Перечень вопросов для проверки конечного уровня знаний:
1. Опишите модельные липидные мембраны. Где они используются?
2. Охарактеризуйте физические свойства мембран.
3. При фазовом переходе мембранных фосфолипидов из жидкокристаллического состояния в гель толщина бислоя изменяется. Как при этом изменится электрическая емкость мембраны? Как изменится напряженность электрического поля в мембране?
4. Примените уравнение Фика к биологической мембране.
5. Запишите и объясните уравнение Нернста-Планка.
6. Покажите, что уравнение Нернста-Планка сводится к уравнению Фика для диффузии незаряженных частиц.
7. Опишите виды пассивного транспорта.
8. Проницаемость клеточных мембран для молекул воды приблизительно в 10 раз выше, чем для ионов. Что произойдет, если в изотоническом водном растворе, в котором находятся эритроциты, увеличить концентрацию осмотически активного вещества (например, ионов Na+)?
9. Опишите опыт Уссинга.
7.Решите задачи:
1. Какое расстояние на поверхности мембраны эритроцита проходит молекула фосфолипида за 1 секунду в результате латеральной диффузии? Коэффициент латеральной диффузии принять равным 10-12 м2/с. Сравните с окружностью эритроцита диаметром 8 мкм.
2. Удельная электрическая емкость мембраны аксона, измеренная внутриклеточным микроэлектродом, оказалась равной 0,5 мкФ/см2. По формуле плоского конденсатора оцените толщину гидрофобного слоя мембраны с диэлектрической проницаемостью 2.
3. Толщину двойного слоя на границе мембрана — электролит характеризует дебаевский радиус δ. Определите δ для случая, когда в растворе электролита, окружающем мембрану, есть только ионы калия с концентрацией: 1) 10-5 моль/л; 2) 10-2 моль/л.
4. Найдите дебаевский радиус экранирования, создаваемого присутствующими в растворе ионами кальция с концентрацией 10-5 моль/л и натрия с концентрацией 10-4 моль/л. Как изменится δ, если в растворе будут только ионы кальция в концентрации 10-4 моль/л?
5. Критический радиус липидной поры в мембране зависит от краевого натяжения поры, поверхностного натяжения мембраны и мембранного потенциала. Выведите формулу для критического радиуса поры. Рассчитайте критический радиус поры при отсутствии мембранного потенциала. Принять краевое натяжение поры 10-11 Н, поверхностное натяжение липидного бислоя 0,3 мН / м.
6. Молярная концентрация кислорода в атмосфере са = 9 моль/м. Кислород диффундирует с поверхности тела насекомых внутрь через трубки, называемые трахеями. Длина средней трахеи равна приблизительно h = 2 мм, а площадь ее поперечного сечения S = 2∙10-9 м2. Считая, что концентрация кислорода внутри насекомого (с) в два раза меньше, чем концентрация кислорода в атмосфере, вычислите поток диффузии через трахею. Коэффициент диффузии кислорода D = 10-5 м2/с.
7. Двойной фосфолипидный слой уподобляет биологическую мембрану конденсатору. Вещество мембраны представляет собой диэлектрик с диэлектрической проницаемостью ε = 4. Разность потенциалов между поверхностями мембраны U = 0,2 В при толщине d = 10 нм. Рассчитайте электроемкость 1 мм2 мембраны и напряженность электрического поля в ней.
8. Площадь поверхности клетки приблизительно равна S=5∙10-10 м2. Удельная электроемкость мембраны (емкость единицы поверхности) составляет Суд = 10-2 Ф/м2. При этом межклеточный потенциал равен U = 70 мВ. Определите: а) величину заряда на поверхности мембраны; б) количество одновалентных ионов, образующих этот заряд.
9. Фермент Na+ - К+ - АТФаза в плазматической мембране эритроцита совершил шесть циклов. Какое количество ионов натрия и калия при этом было активно транспортировано? Сколько энергии было при этом израсходовано, если гидролиз одного моля АТФ сопровождается освобождением 33,6 кДж? Эффективность процесса энергетического сопряжения считать 100 %.
8. Самостоятельная работа студентов:
По учебнику Антонова В.Ф.и др. (§ 15.4.) ознакомтесь с физическими методами определения толщины мембраны.
9. Хронокарта учебного занятия:
1. Организационный момент – 5 мин.
2. Разбор темы – 50 мин.
3. Решение ситуационных задач – 40 мин.
4. Текущий контроль знаний – 30 мин
5. Подведение итогов занятия – 10 мин.
10. Перечень учебной литературы к занятию:
1.Ремизов А.Н., Максина А.Г., Потапенко А.Я. Медицинская и биологическая физика, М., «Дрофа», 2008, §§ 11.1, 11.2, 11.5, 11.6.
2.Физики и биофизика.(под ред. Антонова В.Ф.). М., «ГЭОТАР-Медиа», 2008, §§ 15.1-15.8, 16.1-16.3.
Основные проблемы и понятия метрологии
Измерением называют нахождение значения физической' величины опытным путем с помощью технических средств. Измерения позволяют установить закономерности природы и являются элементом познания окружающего нас мира.
Различают измерения прямые, при которых результат получается непосредственно из измерения самой величины (например, измерение температуры тела медицинским термометром, измерение длины предмета линейкой), и косвенные, при которых искомое значение величины находят по известной зависимости между ней и непосредственно измеряемыми величинами (например, определение массы тела при взвешивании с учетом выталкивающей силы, определение вязкости жидкости по скорости падения в ней шарика). Технические средства для производства измерений (средства измерений) могут быть разных типов. Наиболее известным читателю средством измерений является измерительный прибор, в котором измерительная информация представляется в форме, доступной для непосредственного восприятия наблюдателем (например, температура представлена в термометре длиной столбика ртути, сила тока — показанием стрелки амперметра или цифровым значением). К средствам измерений относят также и меру, которая предназначена для воспроизведения физической величины заданного размера (например, гиря определенной массы).
Одно из распространенных средств измерений — измерительный преобразователь (датчик). Он предназначен для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения (например, температура может быть представлена электрическим сигналом).
начение физической величины, полученное при измерении, отличается от истинного. Степень приближения результатов измерения к истинному значению измеряемой величины характеризуется точностью измерений. Точность измерений является качественным показателем измерений.
Количественная оценка результата измерений дается абсолютной погрешностью — отклонением результатов измерений от истинного значения измеряемой величины. Чем меньше погрешность, тем выше точность измерений.
Погрешности объясняются несовершенством средств измерений, неопытностью персонала, влиянием посторонних факторов и др. Из этих причин можно выделить те, которые проявляются нерегулярно и при повторных измерениях оказывают случайное количественное воздействие на результат. Такие факторы приводят к случайным погрешностям. Это случайные величины, поэтому их можно обработать, проанализировать и таким образом учесть, используя соответствующий математический аппарат: теорию вероятностей и математическую статистику (см. гл. 2 и 3).
Сведения по теории погрешностей, необходимые студентам-медикам, приведены в [1].
Одним из основных метрологических понятий является единица измерения физической величины. Единицей измерения физической величины называют стандартное значение этой физической величины, принятое по соглашению в качестве основы для ее количественной оценки.
Единицы физических величин в основном группируются в системы единиц. Основной является Международная система единиц (система интернациональная, СИ). Справочный материал по единицам физических величин приведен в [2]. Не останавливаясь на этих вопросах, рассмотрим лишь относительные и логарифмические величины.
В физических измерениях достаточно широкое распространение получили относительные величины, которые являются отношением физической величины к одноименной физической величине, принимаемой за исходную. В качестве примера можно указать концентрацию раствора, диэлектрическую и магнитную проницаемости, коэффициент полезного действия, относительную деформацию, коэффициент трения, вязкость крови относительно вязкости воды и т. д.
Единицы измерения относительных величин не имеют размерности и названия. Однако в ряде случаев относительную величину традиционно выражают со стократным или тысячекратным увеличением. При этом соответствующая единица измерения будет иметь название: процент (%) или промилле (%о).
Для выражения уровня звукового давления, уровня интенсивности звука, уровня усиления электрического сигнала и т. п. удобнее использовать логарифм относительной
величины (наиболее распространен десятичный логарифм):
 |
где а1 и а2 — одноименные физические величины.
Единицей логарифмической величины является бел (Б):
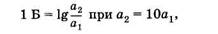 |
если а — «энергетическая» величина (мощность, интенсивность, энергия и т. п.), или
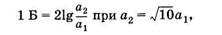 |
если а — «силовая» величина (сила, механическое напряжение, давление, напряженность электрического поля и т. п.).
Достаточно распространена дольная единица — децибел (дБ): 1дБ = 0,1Б.
Заметим, что 1 дБ соответствует соотношению «энергетических» величин а2 ≈ 1,26а1:
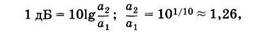 |
а для «силовых» величин а2 ≈ 1,12а1:
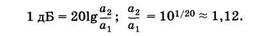 |
Дата добавления: 2015-03-03; просмотров: 1525;
