Специальная теория относительности

Еще в классической механике был известен принцип относительности Г. Галилея: «Если законы механики справедливы в одной системе координат, то они справедливы и в любой другой системе, движу­щейся прямолинейно и равномерно относительно первой». Такие системы называются инерциальными, поскольку движение в них подчиняется закону инерции (первый закон Ньютона). Общепринятая формулировка первого закона Ньютона та­кова: «Существуют системы отсчета, относительно которых всякое тело сохраняет состояние своего движения (состоя­ние покоя или равномерного прямолинейного движения), пока действие всех тел и полей на него компенсировано».

Если мы имеем хотя бы одну такую инерциальную систе­му отсчета, то всякая другая система отсчета, которая дви­жется относительно первой равномерно и прямолинейно, также является инерциальной. Все другие системы отсче­та называются неинерциальными. Под системой отсчета понимается тело отсчета, от­носительно которого рассматривается движение, связанная с телом отсчета система координат (например, декартова си­стема координат, состоящая из трех взаимоперпендикуляр­ных пространственных координатных осей), и заданный способ определения времени.

Рассмотрим покоящуюся инерциальную систему отсчета К и другую инерциальную систему отсчета К', движу­щуюся относительно К равномерно и прямолинейно со скоростью V, много меньшей скорости света (рис. 1). Пусть оси X и X' обеих рассматри­ваемых систем отсчета совпадают, а оси Y и Y; Z и Z' со­ответственно параллельны.

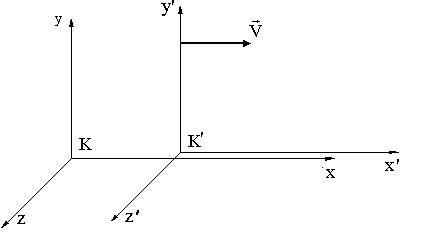
Рис. 1. Инерциальные системы К и К', движущиеся относительно друг друга.

Таким образом, система К' движется со скоростью V относительно К вдоль оси X. Положение некоторой точ­ки (тела) в системах отсчета выражается значениями де­картовых координат в соответствующих системах отсчета. Легко видеть, что между ними имеется следующая зависи­мость:

X = X' + Ut; Y= Y'; Z = Z' (1)

Скорости движе­ния тела относительно обеих систем отсчета:

U= U' + V (2)

Скорость относительно неподвижной системы отсчета складывается из скорости относительно подвижной систе­мы отсчета и скорости самой системы отсчета.

Если теперь возьмем производную по времени от пра­вой и левой части уравнения (2), то найдем выражение, связывающее ускорения тела относительно обеих систем отсчета. Так как система К' движется равномерно и прямо­линейно относительно К, и скорость U является постоянной величиной, то производная от U по времени равна 0, и мы получаем:

а = а' (3)

Уравнения (1), (2), (3) называются преобразованиями Галилея и описывают, как связаны между собой кинема­тические параметры движения тела при переходе из одной инерциальной системы отсчета в другую. Тот факт, что ускорения тел относительно обеих инерциальных систем отсчета одинаковы, позволяет сделать вывод о том, что законы механики, определяющие причин­но-следственные связи движения тел, одинаковы во всех инерциальных системах отсчета. И это составляет суть принципа относительности Галилея.

В начале XX века выяснилось, что принцип относительности справедлив также в оптике и электродинамике, т.е. в других разде­лах физики. Принцип относительности расширил свое значение и теперь звучал так: законы физики имеют одинаковую форму во всех инерциальных системах отсчета.

После того как физики отказались от представления о сущест­вовании эфира как всеобщей среды, рухнуло и представление об эта­лонной системе отсчета. Все системы отсчета были признаны равно­значными, и принцип относительности стал универсальным. Относительность в теории относительности означает, что все системы отсчета одинаковы и нет какой-либо одной, имеющей преимущества перед другими. Вместе с принципом относительности в физике утвердились понятия ин­вариантности, инвариантов и симметрии, а также связь их с законом сохра­нения и вообще с законами природы. Инвариантность означает неизменность физических величин или свойств природных объектов при переходе от одной системы отсчета к другой.

Экспери­ментальные данные о постоянстве скорости света (согласно опыту Майкельсона-Морли) привели к пара­доксу, для разрешения которого понадобилось введение принципи­ально новых представлений. Пояснить сказанное поможет следующий пример. Предположим, что мы плывем на корабле, движущемся прямолинейно и равно­мерно относительно берега. Все законы движения остаются здесь таки­ми же, как на берегу. Общая скорость движения будет определяться суммой движения на корабле и движения самого корабля. При скоро­стях, далеких от скорости света, это не приводит к отклонению от законов классической механики. Но если наш корабль достигнет скорости, близкой к скорости света, то сумма скорости движения корабля и на корабле может превысить скорость света, чего на самом деле не может быть, так как в соответствии с экспериментом Майкельсона скорость света всегда одинакова во всех системах координат, независимо от того, движется ли излучающий источник или нет.

Рассматривая это противоречие, А. Эйнштейн предложил отка­заться от представления об абсолютности и неизменности свойств пространства и времени. Он ввел следующие постулаты теории относительности:

1. Принцип относительности: все законы природы одинаковы во всех инерциальных системах отсчета.

2. Принцип постоянства скорости света: скорость све­та одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света.

Из этих постулатов специальной теории относительности следует, что длина тела (вообще расстояние между двумя материальными точками) и длительность (а также ритм) происходящих в нем процессов яв­ляются не абсолютными, а относительными величинами. При при­ближении к скорости света все процессы в системе замедляются, продольные (вдоль движения) размеры тела сокращаются, и со­бытия, одновременные для одного наблюдателя, оказываются раз­новременными для другого, движущегося относительно него.

Это подтверждается преобразованиями Лоренца, которые ученый вывел для подтверждения гипотезы о сокращении размеров тела в направлении их движения относительно эфира. Эйнштейн наполняет пре­образования Лоренца новым физическим содержанием. Так, если Лоренц рассматривал сокращение линейных размеров движущихся тел как действительное сокращение по отношению к неподвижному эфиру, то Эйнштейн рас­сматривает это сокращение как кажущееся для наблюда­теля, относительно которого тело движется. Сокращение линейных размеров тел и замедление длительности вре­менных интервалов — это следствие различных процессов измерения, которыми пользуются различные наблюдатели в различных системах отсчета. Итак, два постулата принципа относительности должны быть допол­нены преобразованиями Лоренца. При скоростях систем отсчета v, близких к скорости света c имеем:

l = l'√(1-v²/c²);

Δt = Δt'/√(1-v²/c²),

где l – линейный размер тела в системе К;

l' - линейный размер тела в системе К';

Δt – промежуток времени в системе К;

Δt'- промежуток времени в системе К'.

Эйнштейн показал также, что преобразования Лоренца переходят в преобразования Галилея при скоростях, намного меньших скорости света, тем са­мым устанавливая границы применимости классической механики для мира малых скоростей.