Кривая предельных издержек как кривая предложения

До настоящего момента мы считали уровень цен, по которым фирма продает свою продукцию, неизменным по величине. Рассмотрим, каким будет оптимальный выпуск продукции фирмой в случае их изменения (рис. 7.9). Пусть цена продукции последовательно снижается с уровня Р₅ до уровня Р₀:

· при цене Р₅ предприятие будет максимизировать прибыль и производить Q₅ единиц продукции;

· при цене Р₄ фирма окажется в точке безубыточности (нулевой экономической прибыли) и выпустит Q₄ единиц;

· при цене Р₃ предприятие будет минимизировать убытки и производить Q₃ единиц продукции;

· при цене Р₂ фирма попадет в точку безразличия и либо выпустит Q₂ единиц, либо вовсе прекратит производство;

· наконец, при любой цене ниже Р₂ (например, при Р₁) выпуск точно будет остановлен (Q₁ = 0).

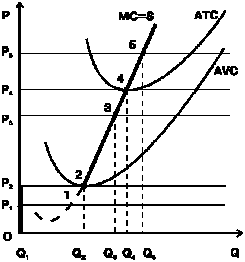
Рис. 7.9. Кривая предложения конкурентной фирмы

Легко заметить, что описывая поведение фирмы при разных уровнях цен, мы фактически описали ее кривую предложения. Ведь кривая предложения как раз и показывает, какой объем продукции будет выпущен при том или ином уровне цен. А поскольку интересы предприятия требуют довести производство до точки, где предельные издержки будут равны цене (MC = P), то кривая предельных издержек конкурентной фирмы в краткосрочном периоде будет одновременно ее кривой предложения для этого периода.

Но предприятие выпускает продукцию только в том случае, если рыночная цена превышает минимальные средние переменные издержки (P > АVC_min). Следовательно, кривая предложения продукции (S) в краткосрочном периоде графически ограничивается только тем отрезком кривой предельных издержек (МС), который расположен над минимальной точкой кривой средних переменных издержек. Или, другими словами, кривая предложения совпадает с кривой предельных издержек только при МС > AVC_min. При более низком уровне рыночных цен (P < AVC_min) кривая предложения претерпевает разрыв и в дальнейшем сливается с осью цен (OP).

На графике вся кривая предложения выделена жирной линией.