Спрос и цена

Закон спроса устанавливает обратную зависимость между ценой и объемом продукции, которую хотят купить потребители. Тем самым этот закон провозглашает цену главным фактором, определяющим размеры спроса. Но хозяйственная практика убеждает нас в обратном: в рыночной экономике¹ спрос в большой степени определяется ценой. Не случайно, если не принимать в расчет экстремальные ситуации, именно цена в первую очередь интересует потребителя, решившего купить товар. А все другие характеристики обязательно рассматриваются через призму цен (вспомним, как мы рассуждаем, например, о такой важнейшей характеристике, как качество: дорогой автомобиль, но он своих денег стоит).

Зависимость между ценой товара и спросом на него можно представить табличным, графическим и функциональным способами. Допустим, нам известно, сколько килограммов колбасы может быть продано в соседнем универсаме за неделю при различных уровнях цен. Тогда зависимость между ценой и спросом можно представить в виде таблицы.

Эта же зависимость может быть представлена в виде графика в координатах цен на колбасу (Р ¾ независимая переменная) и количества купленной колбасы (Q ¾ зависимая переменная²) (рис. 4.1.). Для построения графика используем данные нашего гипотетического примера (табл. 4.1)

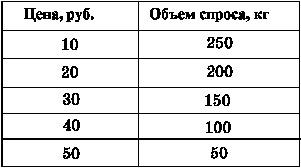
Таблица 4.1. Условный пример связи размера спроса на колбасу с ее ценой

Линия D носит название кривой спроса. Она показывает, какое количество (Q) товара готовы купить покупатели:

а) при каждом данном уровне цен;

б) в конкретный период времени;

в) при неизменных прочих факторах.

Другими словами, движение вдоль кривой спроса (от одной точки к другой) отражает изменение в количестве товара, на которое потребители предъявляют спрос, происходящее в результате изменения цены товара.

Функциональная зависимость между объемом спроса (Q_D) и ценой может быть представлена также в аналитической форме, т. е. в виде формулы

Q_D = f (P).

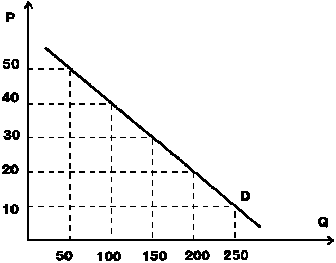
Рис. 4.1. Зависимость спроса от цены

Впрочем, в такой общей форме она не отражает обратной зависимости между спросом и ценой, и при практическом применении формулу необходимо конкретизировать. Например, если зависимость линейная, она примет вид:

Q_D = a - bP,

где a, b ¾ численные коэффициенты.

В нашем условном примере она будет выглядеть следующим образом:

Q_D = 300 - 5Р.