Лекция 1: Понятие интеллектуальной информационной системы (ИИС), основные свойства.
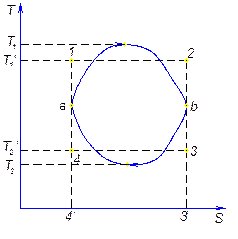
Рассмотри произвольный цикл и цикл Карно с эквивалентной совершённой работой. Площади фигур в координатах T-s равны.
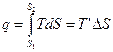
T’ – термодинамическая температура
Т2’ – средняя Т° отводимого тепла
В результате получим вместо произвольного цикла эквивалентный цикл Карно 1234.
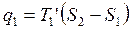
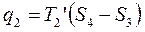
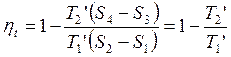
Термический КПД произвольного цикла равен термическому КПД цикла Карно, взятому при средних температурах подвода и отвода тепла.
В идеале необходимо стремиться к увеличению Т1’ и уменьшению T2’.
Докажем, что в заданном интервале температур термический КПД цикла Карно – максимальный.
> 
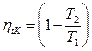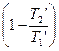, т.к. Т1’ < T1 T2’ > T2
htK > ht
Цикл Карно – есть идеальный цикл по величине htK по его значению судят о предельно возможном КПД реального двигателя.
Пример: Определить максимально возможный КПД двигателя, в котором Т1=1800°С Т2=27°С
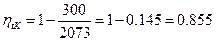
Обобщенный цикл Карно. Регенерация тепла в цикле.
Обобщенный цикл Карно – цикл, состоящий из из 2-х изотерм и 2-х эквидистантных политроп.
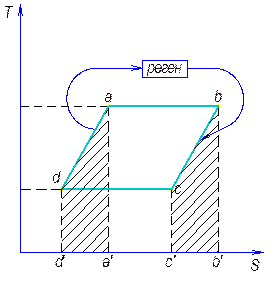
аб – расширение 
Подводимое тепло q1= abb’a’
сd – сжатие
Отводимое тепло q2= cdd’c’
qbc – отводится тепло …
qdc – подводится тепло из …
Т.к. bc и dc – эквидистантны, то:
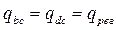
За цикл от окружающей среды поступает только:
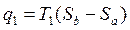
Отводится в среду за цикл:
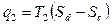
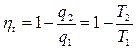
Термический КПД этого цикла равен термическому КПД цикла Карно.
Регенерацией тепла в циклах называется использование тепла, взятого на одном участке цикла, для совершения процесса на другом участке цикла с одинаковыми температурами.
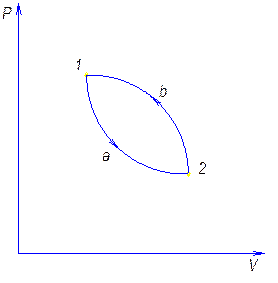
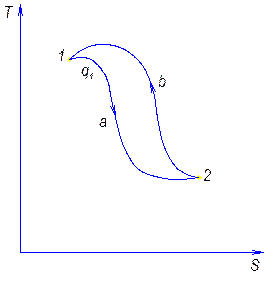
Обратный цикл и его характеристика.
Обратным называют цикл, который в координатных осях совершается против часовой стрелки.
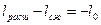
В результате такого цикла передается тепло от среды с меньшей температурой к среде с большей температурой.
Характеристикой этого цикла является холодильный коэффициент e.
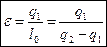
Математическое выражение II-го закона термодинамики. Характеристика обращенных процессов.
Для цикла Карно: Для любого цикла:
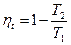
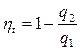
Следовательно, для цикла Карно:
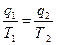q2 – всегда с минусом.
Поэтому:
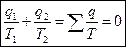(1)
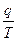- приведенная теплота, следовательно, для цикла Карно сумма приведенных теплот =Q.
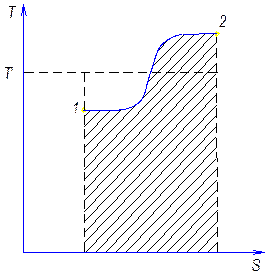
Теперь установим аналогичную характеристику для цикла произвольной формы. Пусть в диаграмме T-S имеем произвольный прямой обратимый цикл для 1 …
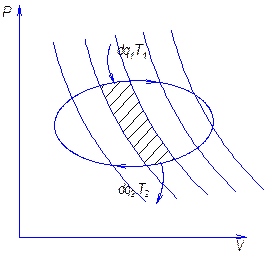
Проведем ряд адиабат, в результате цикл разбили на ряд элементарных циклов, в каждом из которых 2 адиабаты и 2 приведенных участка. Вследствие малости криволинейные участки можно заменить изотермами, получим цикл Карно.
Совокупность элементарных циклов заменит исходный цикл, т.к. адиабаты как бы уничтожат друг друга.
Тепло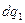 
подводится 
и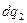 
отводится при 
.
На основании уравнения (1)
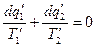
для 2 – го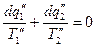 
и т.д.
Пройдя весь контур: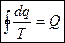 
(2)
(2) является математической характеристикой обратимых циклов.
Следствие из уравнения (2)
1.Энтропия есть параметр состояния для любого веществ, т.к. если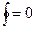 
, то подынтегральная функция есть полный дифференциал, т.е. дифференциальный – параметр состояния.
При выводе уравнения (2) мы брали любое рабочее тело, поэтому и параметры S – свойство любого рабочего тела.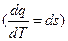 
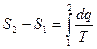(3)
(3) – только для обратимых циклов.
Отчет энтропии ведут от нормального состояния газа. Поэтому:
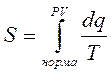
PH=760 мм Hg
TH=273 °K
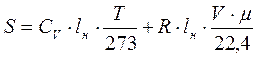
2. Энтропия адиабатно изолированной системы, в которой совершается обратимые циклы, остается постоянной:
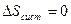
Это следствие вытекает из определение обратимого процесса и из равенства:
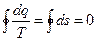
Характеристика необратимых процессов.
|
В диаграмме T –S дан необратимый цикл совершаемый любым рабочим телом, произвольно.
Необратимость отразим конечной разностью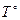 
рабочего тела и источников.
В результате проведения адиабат получим элементарные циклы.
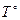подвода можно считать изетормой.
В результате получим необратимый цикл Карно:
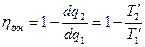
dq1 – подводимое; dq2 – отводимое; кн – цикл Карно необратимый.
Если бы цикл был обратимый, то он совершался бы в интервале температур от T1 до T2:
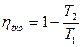но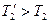 
; 
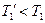
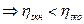
тогда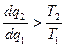 
и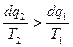 
т.к. q2 всегда отрицательное. 
.
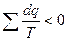Пройдя по всему контуру исходного цикла можно написать:
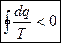(4) – для необратимых циклов;
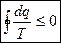(5) – объединяем (2) и (4)
Изменение энтропии при необратимом процессе.
1а2 – необратимый процесс
2в1 – обратимый процесс
В условии цикл необратимый, поэтому на ос
нование (4):
интервале температур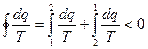 
для 2в1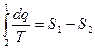 
и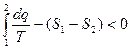 
, и тогда 
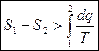(6)
? интеграл ? изменения энтропии, поэтому расчет нельзя вести количественно по конечным разностям.
Применительно к адиабатному процессу:
.
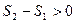
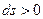1 – 2 – обратимый адиабатный процесс;
1` - 2` - необратимый адиабатный процесс.
Необратимый процесс всегда идет с увеличенем энтропии.
Пример:
TA>TB
QA=QB; Определить изменение энтропии
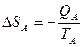
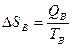, следовательно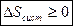 
В теплоизолированной системе энтропия системы может увеличиваться или оставаться постоянной, но никогда не уменьшаться.
Работоспособность и энергетические потери.
Работоспособность – количество работы, которую можно подсчитать при заданных источниках тепла.
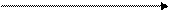
1 – 2 – производится тепло.
Из предыдущих рассуждениях получаем что механическая работа получается при холодном источнике окружающей среда Tокр.
При адиабатном сжатии и расширении: цикл 1-2-3-4.
Р – работоспособность
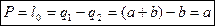
Расчет энергетических потерь.
Это есть потери полезной работы вследствие необратимых явлений.
Оцениваются они:
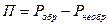П – потери работоспособности.
Для расчета используется свойство роста энтропии.
Пусть энергетические потери обусловлены только трением газа при расширении. Трение происходит как у поверхности, так и внутри; вследствие разности скоростей отдельных струек. Трение – явно необратимое явление, т.к. тепла, затраченного на трение недостаточно в силу II закона термодинамики для получение работы, затраченной на трение. ( ht<1). Особенно значим этот вопрос (о трении газа) в реактивной техники, где большие скорости.
1-2 – обратимый подвод тепла;
2-3 – обратимое адиабатное расширение;
3-4 – обратимый отвод тепла при Tокр среды;
4-1 – обратимое адиабатное сжатие.
Рассмотрим, как повлияет трение в процессе 2-3. Энтропия увеличивается, по сравнению с обратимым расширением. Условно обозначим пунктиром 3` - конец расширения.
Работоспособность при обратимом процессе:
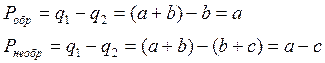
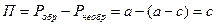, но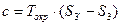 
Докажем, что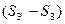 
выражает изменение энтропии всей системы за цикл, т.е.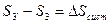 
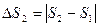- уменьшение энтропии горячего источника тепла
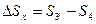- увеличение энтропии холодного источника тепла
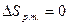- изменение энтропии рабочего тела за цикл
Следовательно: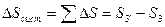 
(т.к.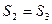 
) итак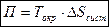 
Потери работоспособности подсчитываются как произведение наименьшей температуры системы на увеличение энтропии системы.
Изменение энтропии не только мера необратимости процесса, но и величина, позволяющая рассчитать энергетические потери.
Энтропия – параметр состояние или физическое свойство вещества. Это свойство заключается в способности системы рассеивать тепловую энергию, не давая ей превращаться в работу. Энтропию нельзя измерить, т.к. пока не созданы приборы, но ее можно рассчитать по другим параметрам состояния. Энтропия имеет размерность теплоемкости, но другой физический смысл.
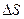- показывает количество тепла, которое рассеяно системой, приходящееся на 1°.
Реальные газы.
Наибольшее распространение получили СО2 , NH3 , H2O , пары других жидкостей – все они не подходят под определение идеальные газы. При расчете чаще пользуются таблицами и диаграммами.
Рассмотрим уравнение состояния для реальных газов:
Уравнение Ван-дер-Ваальса.
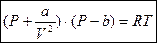
a и b – const для каждого вещества; определяются опытным путем.
Если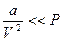 
; 
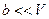, то 
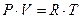- уравнение Менделеева – Клапейрона.
b – поправка к удельному объему, учитывающая конечные размеры молекул в газе.
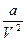- учитывает силы притяжения между молекулами, которые действуют в ?????? давлении, что и внешнее.
Это уравнение широко используется для качественного исследования рабочих тел.
Водяной пар.
Одно из самых распространенных рабочих тел. Применяется во многих целях. Широко распространен, безвреден, обладает приличными термодинамическими свойствами.
Рассмотрим парообразование при постоянном давлении.
За начальные параметры примется: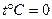 
, 
.
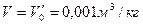Разделим процесс на 3 стадии:
1 стадия – А0 – А` - нагревание воды до кипения (до tн). V` - удельный объем кипящей воды.
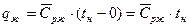
т.к. процесс при P=const, то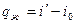 
, откуда 
; 
.
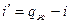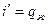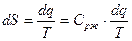
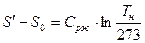
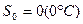
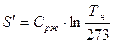
2 стадия – A` - A`` - кипение жидкости (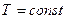 
), поэтому линия кипения A` - A`` горизонтальная.
В результате подвода и отвода тепла увеличивается количество пара и уменьшается количество воды.
A`` - характеризует состояние сухого пара.
R – Теплота парообразования.
Т.к.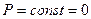 
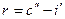
V`` - удельный объем сухого насыщенного пара.
На T – S диаграмме отметим:
.
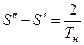
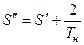Точки A` - A``. Например: A`x характеризует состояние влажности пара содержащего капельки жидкости. Влажный пар характеризуется степенью сухости x=qпара.
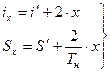для влажного пара
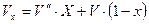- объем влажного пара
В технических расчетах часто считают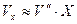 
(при невысоких давлениях до 40 ат.).
3 стадия – A`` - A – осуществляется не в котлах, а в устройствах – пароперегревателях.
V – удельный объем перегретого пара.
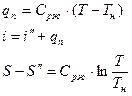
Для более высокого давления.
Соединим на диаграммах сходственные точки и получим 3 линии.
1 – характеризует состояние воды при 0°С и при различных Р. Давление на диаграмме T – S превратится в точку A0.
2 – характеризует состояние кипящей воды; степень сухости Х=0 – нижняя пограничная кривая.
3 – характеризует состояние сухого пара; Х=1 – верхняя пограничная кривая.
К – критическая точка - соединение линий 2 и 3 состояние здесь критическое.
Для воды:
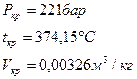
Таблицы и диаграммы для водяного пара.
Таблицы:
а) Для кипящей воды и сухого насыщенного пара параметры определяются по T или P.
Все параметры кипящей воды ( ` ); сухого насыщенного пара ( `` ).
б) Для перегретого пара параметры определяются двумя: P и t.
Диаграммы P – V и T – S используются в исследовательских целях.
При Х=0 критической точке расчеты не производятся. Ниже кривой Х=0 – влажный пар.
Рассмотрим адиабатный процесс расширения
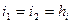- адиабатный или ??? ??????
Величина технических работ.
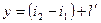
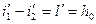
Течение газов и паров.
Роль течений возросла с развитием турбинных и реактивных двигателей. Теория течения базируется на термо- и аэродинамике. Все устройства, в которых происходят течения, ???
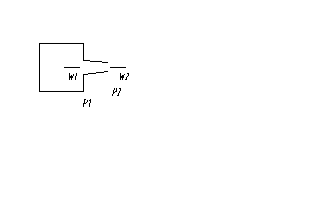
а) Сопла
б) Диффузоры
Основные уравнения течения.
1. уравнение неразрывности потока (сплошности).
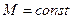- массовый расход; установившийся режим течения.
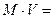
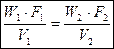(1)
2. уравнение энергии.
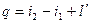
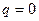
Течение газов и паров считается адиабатным. Если нет рабочих органов в аппарате, то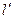 
работа равна располагаемой работе:
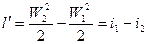
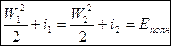(2).
В любом течении сумма кинетической энергии и энтальпии потока одинаков и равна полной энергии:
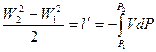
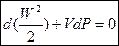(3).
Из (3) следует:
¾ в сопле давление уменьшается
¾ в диффузоре давление увеличивается.
Адиабатное течение в сопле.
Увеличение скорости за счет уменьшения давления. Истечение из большого резервуара.
Лекция 1: Понятие интеллектуальной информационной системы (ИИС), основные свойства.
Основные вопросы лекции:
1. Цель преподавания дисциплины. Терминология
2. История развития систем искусственного интеллекта.
3. Основные определения теории искусственного интеллекта: информация и данные, знания, база знаний, информационные модели знаний, искусственный интеллект.
4. Классификация интеллектуальных систем
Дата добавления: 2015-02-28; просмотров: 831;