Настилы перекрытий
1.По данным, представленным в таблице ниже, изучается зависимость объема валового национального продукта Y (млрд. долл.) от следующих переменных: X1 – потребление, млрд.долл. Х2 – инвестиции, млрд. долл.
Таблица 5.14 - Исходные данные
| Y | 9,5 | 16,5 | ||||||||
| X1 | 1,65 | 1,8 | 2,0 | 2,1 | 2,2 | 2,4 | 2,65 | 2,85 | 3,2 | 3,55 |
| Х2 | 23,5 | 26,5 | 28,5 | 30,5 |
1.Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии. Дайте экономическую интерпретацию параметров модели. Определите коэффициент эластичности
2.Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.
3.Получите прогнозные значения валового национального продукта при сохранении средних темпов роста потребления и инвестиций.
4.Используя статистические данные, проведите аналогичные расчеты для РФ за период 1997-2007 гг.
2.По статистическим данным изучается зависимость оборота розничной торговли Y (млрд. долл.) от ряда факторов. В таблице представлены следующие данные: Y – оборот розничной торговли, млрд.руб.; Х1 – денежные доходы населения, млрд.руб.; Х2 – денежные расходы на покупку товаров и услуг, млрд.руб.; Х3 – численность безработных, тыс.чел.
1. Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
2. Дайте экономическую интерпретацию параметров модели. Рассчитайте коэффициенты эластичности. Определить стандартизированные коэффициенты регрессионной модели.
Таблица 5.15 - Исходные данные
| Годы | Y | X1 | X2 | X3 |
| 5100,3 | 3888,6 | |||
| 6684,3 | ||||
| 3983,9 | 3009,4 | 7059,1 | ||
| 5001,8 | 6287,9 | |||
| 8900,5 | 6147,3 | 6154,7 | ||
| 10976,3 | 7670,7 | 5683,3 | ||
| 13522,5 | 9615,3 | 5775,2 | ||
| 5208,3 | ||||
| 14675,3 | 10781,3 | 5222,5 | ||
| 15325,7 | 11562,8 | 2156,7 |
3. Получите прогнозные значения результативного показателя в зависимости от средних темпов прироста факторных показателей.
4. Проведите аналогичный расчет на материалах одного из регионов РФ.
3. По регионам одного экономического района приводятся данные за 2008 год (табл. 5.16).
Таблица 5.16 - Исходные данные
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб, х | Среднедневная заработная плата, руб, у |
Рассчитайте линейное уравнение парной регрессии у от х, среднюю ошибку аппроксимации. В регионе 1 прогнозируемая величина прожиточного минимума - 100 руб,, сколько должна составить среднедневная заработная плата?
4.Рассчитать параметры производственной функции отрасли «пищевая промышленность». Использовать модификацию производственной функции с автономным темпом технического прогресса. На основе полученной модели сделать вывод об уровне экономического развития отрасли и о перспективах ее развития. Получить линейное уравнение, связывающее темпы прироста основных факторов производства и прироста валовой продукции. Оценить адекватность полученной модели и разработать прогноз развития отрасли в трех вариантах: оптимистичный, пессимистичный и наиболее вероятный. Используйте генетический и нормативно-целевой подходы к прогнозному процессу.
Таблица 5.17 - Показатели экономического состояния пищевой промышленности
| год | |||||||||
| Валовый выпуск, млн руб.,Y | |||||||||
| Стоимость основных фондов, млн руб.,F | |||||||||
| Численность ППП, в т.ч. рабочие, тыс чел.,L | 29,2 | 23,4 | 20,8 | 20,0 | 23,0 | 20,4 | 18,5 | 15,9 | 14,5 |
5.Производственная функция Кобба-Дугласа характеризуется следующим уравнением: 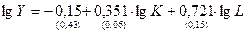 .
. 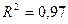 .
.
В скобках указаны значения стандартных ошибок для коэффициентов регрессии.
1. Оцените значимость коэффициентов модели по t-критерию Стьюдента и сделайте вывод о целесообразности включения факторов в модель.
2. Запишите уравнение в степенной форме и дайте интерпретацию параметров.
3. Что можно сказать об эффекте от масштаба производства?
6.Для функции y=a0*elt*La*Kb получены значения: a0= 1,038;
l= - 0,0294; a= 0,2399; b= 0,9749. Темпы прироста связаны уравнением: Py= -0,0294+0,2399*PL+0.9749*PK . Делаем допущение (принимаем гипотезу), что прироста занятости в производственной сфере не будет. Определите необходимый прирост капитала для обеспечения ежегодного прироста конечного продукта на 4%.
7.Имеются данные о вариантах производства 100 млн. руб. продукции при различных значения затрат труда (тыс. чел.) и стоимости основных производственных фондов (млн. руб.). Задание:
1. На основе графиков, построенных для аргументов функции 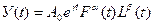 сформулировать гипотезу о возможных значениях
сформулировать гипотезу о возможных значениях 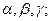 . Рассчитать параметры производственной функции и проверить адекватность модели. Сравнить гипотетические значения с расчетными.
. Рассчитать параметры производственной функции и проверить адекватность модели. Сравнить гипотетические значения с расчетными.
Таблица 5.18 - Исходные данные
| t | ||||||||
| У(t) | ||||||||
| F(t) | 9,2 | 7,5 | 6,8 | 5,5 | 4,2 | 2,1 | ||
| L(t) | 2,2 | 3,1 | 3,9 | 4,7 | 5,8 | 7,6 | 9,3 |
2. Используя полученное регрессионное уравнение получить уравнение производительности труда, фондовооруженности, предельной производительности труда.
5. Осуществить целевой прогноз: на основе заданной траектории численности работников и эволюционного значения валового продукта в периоде упреждения определить значение стоимости основных фондов для t = 9, 10, 11.
8. Структурная форма макроэкономической модели имеет вид:
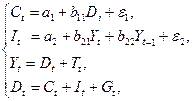
где Сt – расходы на потребление в период t, Yt – чистый национальный продукт в период t, Yt-1 – чистый национальный продукт в период t-1, Dt – чистый национальный доход в период t, It – инвестиции в период t, Tt – косвенные налоги в период t, Gt – государственные расходы в период t.
Задание:
1. Проверьте каждое уравнение модели на идентифицируемость, применив необходимое и достаточное условия идентифицируемости.
2. Запишите приведенную форму модели.
3. Определите метод оценки структурных параметров каждого уравнения.
9. Одна из модификаций модели спроса – предложения имеет вид:
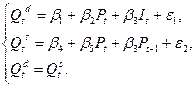
где Qdt – предложение товара в период t, 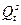 - спрос на товар в период t, Рt – цена товара в период t-1, Рt-1 – цена товара в период t-1, It – доход в период t.
- спрос на товар в период t, Рt – цена товара в период t-1, Рt-1 – цена товара в период t-1, It – доход в период t.
Задание:
1. Проверьте каждое уравнение модели на идентифицируемость, применив необходимое и достаточное условия идентифицируемости.
2. Запишите приведенную форму модели.
3. Определите метод оценки структурных параметров каждого уравнения.
10.Изучается модель вида
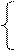 y=a1+b1∙ (C+D)+ε1;
y=a1+b1∙ (C+D)+ε1;
C=a2+b2∙y+b3∙y-1+ ε2,
где y – валовой национальный доход; у–1 – валовой национальный доход предшествующего года; С – личное потребление; D – конечный спрос (помимо личного потребления); ε1и ε2– случайные составляющие.
Информация за девять лет о приростах всех показателей дана в табл. 5.19.
Таблица 5.19 - Темпы прироста макроэкономических показателей
| Год | D | y–1 | y | С | Год | D | y–1 | y | С |
| –6,8 | 46,7 | 3,1 | 7,4 | 44,7 | 17,8 | 37,2 | 8,6 | ||
| 22,4 | 3,1 | 22,8 | 30,4 | 23,1 | 37,2 | 35,7 | 30,0 | ||
| –17,3 | 22,8 | 7,8 | 1,3 | 51,2 | 35,7 | 46,6 | 31,4 | ||
| 12,0 | 7,8 | 21,4 | 8,7 | 32,3 | 46,6 | 56,0 | 39,1 | ||
| 5,9 | 21,4 | 17,8 | 25,8 | ∑ | 167,5 | 239,1 | 248,4 | 182,7 |
Для данной модели была получена система приведенных уравнений:
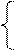 y=8,219+0,6688∙D+0,261∙y-1;
y=8,219+0,6688∙D+0,261∙y-1;
C=8,636+0,3384∙D+0,202∙y-1.
Задание: провести идентификацию модели и рассчитать параметры первого уравнения структурной модели.
11. Модель протекционизма Сальватора (упрощенная версия) выглядит следующим образом:
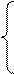 Mt=a1+b12∙Nt+b13∙St+b14∙Mt-1+ ε1;
Mt=a1+b12∙Nt+b13∙St+b14∙Mt-1+ ε1;
Nt=a2+b21∙Mt+b23∙St+b26∙Yt+ ε2;
St=a3+b31∙Mt+b32∙Nt+b37∙Xt+ ε3,
где М – доля импорта в ВВП; N – общее число прошений об освобождении от таможенных пошлин; S – число удовлетворенных прошений об освобождении от таможенных пошлин; Е – фиктивная переменная, равная 1 для тех лет, в которые курс рубля на международных валютных рынках был искусственно завышен, и 0 – для всех остальных лет; Y – реальный ВВП; Х – реальный объем чистого экспорта; t – текущий период; t–1 – предыдущий период.
В таблице 5.20 приведены исходные данные для решения системы линейных уравнений.
Таблица 5.20 - Исходные данные
| Текущий период, t | Реальный ВВП, Y | Доля импорта в ВВП, M | Общее число прошений об освобождении от таможенных пошлин, N | Число удовлетворенных прошений об освобождении от пошлин, S | Фиктивная переменная, E | Реальный объем чистого экспорта, X |
| 1398,5 | 0,129471 | 185,6 | ||||
| 19005,5 | 0,482632 | |||||
| 171509,5 | 0,304956 | |||||
| 610745,2 | 0,232131 | |||||
| 0,242857 | ||||||
| 0,205965 | ||||||
| 0,209359 | ||||||
| 0,234951 | ||||||
| 0,268908 | ||||||
| 0,249292 | 45 000 | 40 000 | 3 232 388 |
Задание: 1) выделить эндогенные и экзогенные переменные; 2) применив необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое из уравнений модели; 3) определить метод оценки параметров модели; 4) записать приведенную форму модели; определить коэффициенты приведенной формы модели; определить коэффициенты структурной формы модели; 5) проверить значимость полученных уравнений и их коэффициентов. Примечание: для нахождения приведенных уравнений (а также коэффициентов структурных уравнений при применении ДМНК) рекомендуется использовать табличный процессор Excel (надстройка «Анализ данных», функция – расчет уравнения регрессии).
* Методика расчета показателя УСР изложена в параграфе 4.2.
Настилы перекрытий
Представляют собой сплошные ряды досок, служащие основанием чистого пола или самим чистым полом. Их укладывают по промежуточным брускам – лагам или прямо по балкам и прибивают к ним гвоздями. Доски настила чистого пола соединяют кромками в шпунт. Настилы перекрытий работают и рассчитывают на изгиб от действия нагрузок от собственной массы, полезных нагрузок, равных 1,5 кН/м2. в жилых, и не менее 2 кН/м2 (200 кг/м2) в производственных зданиях и сосредоточенных грузов, равных 1,5 кН (150 кг). Максимальный прогиб настила не должен превышать 1/250 пролета. Дополнительно проверяют зыбкость настила. Проверки заключаются в том, что прогиб его от сосредоточенного груза 0,6 кН не должен превышать 0,1 мм.
Дата добавления: 2015-02-28; просмотров: 856;
